95% Confidence Intervals

[Dr.Peterson]

I don't quite get what "95% confident" means?

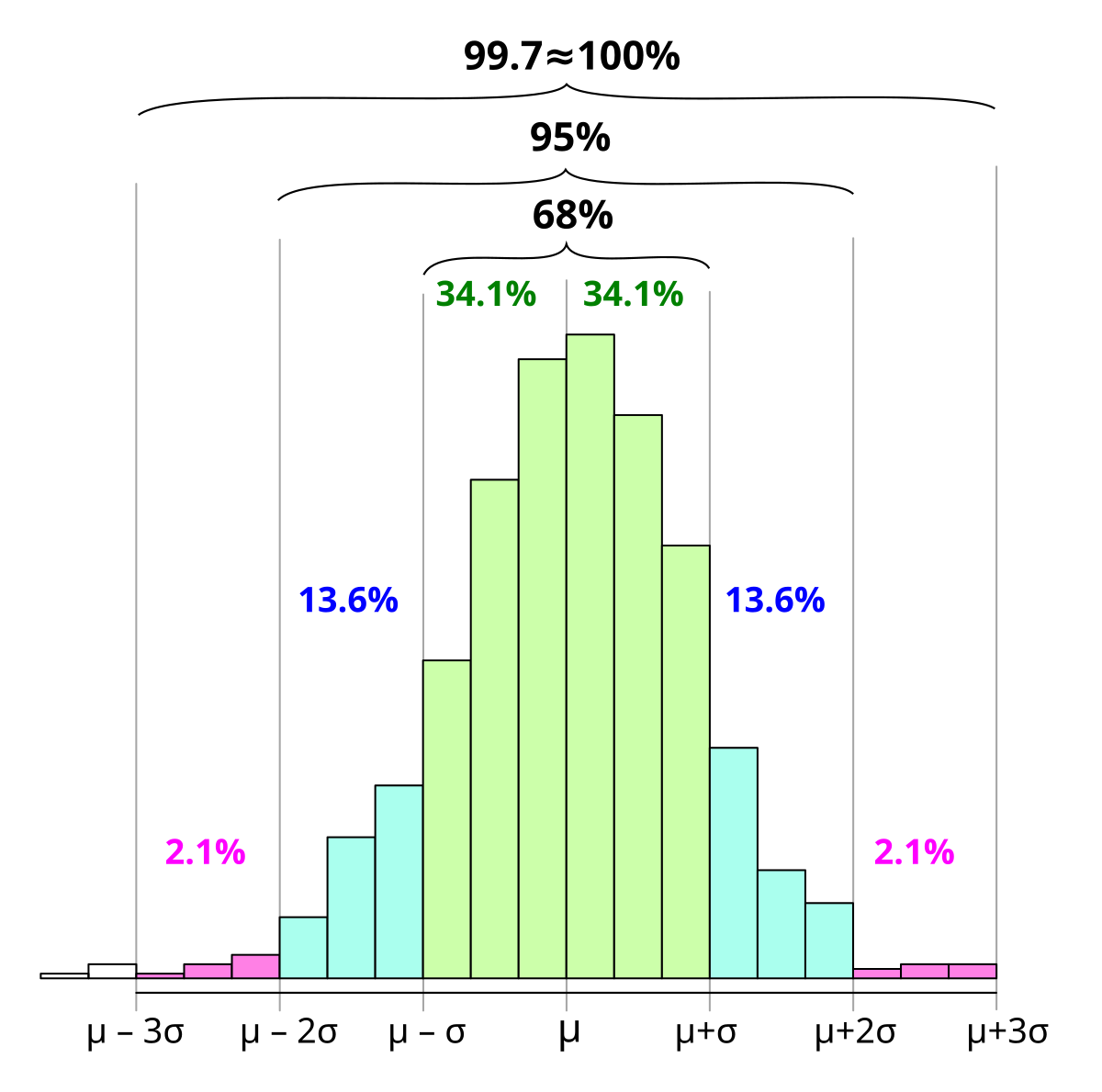
My understanding is that this phrase is defined as a shorthand for the long explanation,

So a 95% confidence interval, say (45, 60), is correctly understood as: repeat the procedure (say) a 100 times (which I suppose means work on a 100 samples), and of the 100 intervals computed thence, 95 will contain the true parameter (95%). This seems to concern itself with the "method" or procedure employed rather any particular interval, which (45, 60) is.

It means that you expect to have gotten it right 95% of the time. This is essentially a subjective probability, as I mentioned:

Now on looking again I find this which says something similar, but then adds,

Recall from the introductory section in the chapter on probability that, for some purposes, probability is best thought of as subjective. It is reasonable, although not required by the laws of probability, that one adopt a subjective probability of 0.95 that a 95% confidence interval, as typically computed, contains the parameter in question.

But, again, I'm not a statistician, so I'm only 90% confident of my answer.

 

[Agent Smith]

shorthand for the long explanation,

Why is there no mention of the interval, in this case (45, 60), which I (had to) calculate(d) in the "longer explanation"?

subjective probability

I don't understand the subjective side to confidence intervals.

I however am aware of subjective probability: it's an interesting topic if nothing else.

 

[Dr.Peterson]

Why is there no mention of the interval, in this case (45, 60), which I (had to) calculate(d) in the "longer explanation"?

Because there's nothing you can say about it! It's just a particular result of the process; it's the process that gives you the "95% confidence".

 

[Agent Smith]

@Dr.Peterson "95% confident that the population parameter is within the interval (45, 60)"?

 

[Agent Smith]

Why?

Sorry, bit confused here. When we compute a 95% confidence interval, we actually have to find the critical z score for 97.5% because the 2 tails constitute the 5% and one tail (2.5% has to be included and the other not). Correct? That's why the critical z value is 1.96 and not 2. Si?

 

[mario99]

Agent Smith, I don't understand why are you confused! Z score points just tell us how far away we are from the mean which allow us to calculate the probability or the area under the curve. For example, the Z-score of [imath]1.96[/imath] allow us to calculate the [imath]Z_{0.975}[/imath] (which has many different names) which just means that the area under the curve is [imath]0.975 \ \text{or} \ 97.5\%[/imath] of the whole area.

In other words, [imath]P(X < 1.96) = 0.975[/imath].

If you want to be more precise:

[imath]\displaystyle P(x < 1.96) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{1.96}e^{-\frac{x^2}{2}} \approx 0.975[/imath]

If you are confused between the Z-score of [imath]1.96[/imath] and the Z-score of [imath]2[/imath] which one of them gives [imath]Z_{0.975}[/imath], just calculate it by the integral or look at it in the Z-score table.

[imath]\displaystyle P(x < 2) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{2}e^{-\frac{x^2}{2}} \ dx \approx 0.977[/imath]

Obviously, it is slightly greater than the [imath]97.5[/imath]th percentile point which is [imath]1.96[/imath].

When they tell you that [imath]95\%[/imath] of the area lies within [imath]1.96[/imath] standard deviation of the mean, they just mean the area under the curve is [imath]0.95[/imath] between [imath]-1.96[/imath] and [imath]1.96[/imath].

Or

[imath]\displaystyle P(-1.96 < X < 1.96) = \frac{1}{\sqrt{2\pi}}\int_{-1.96}^{1.96}e^{-\frac{x^2}{2}} \ dx \approx 0.95[/imath]

This result that I have just shown was the area for a [imath]95\%[/imath] confidence interval.

One last thing to mention is that:

If [imath]P(X < 1.96) = 0.975[/imath], it means [imath]P(X > 1.96) = P(X < -1.96) = 0.025[/imath] which is the area under each of the left and right tails.

 

[Agent Smith]

Agent Smith, I don't understand why are you confused! Z score points just tell us how far away we are from the mean which allow us to calculate the probability or the area under the curve. For example, the Z-score of [imath]1.96[/imath] allow us to calculate the [imath]Z_{0.975}[/imath] (which has many different names) which just means that the area under the curve is [imath]0.975 \ \text{or} \ 97.5\%[/imath] of the whole area.

In other words, [imath]P(X < 1.96) = 0.975[/imath].

If you want to be more precise:

[imath]\displaystyle P(x < 1.96) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{1.96}e^{-\frac{x^2}{2}} \approx 0.975[/imath]

If you are confused between the Z-score of [imath]1.96[/imath] and the Z-score of [imath]2[/imath] which one of them gives [imath]Z_{0.975}[/imath], just calculate it by the integral or look at it in the Z-score table.

[imath]\displaystyle P(x < 2) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{2}e^{-\frac{x^2}{2}} \ dx \approx 0.977[/imath]

Obviously, it is slightly greater than the [imath]97.5[/imath]th percentile point which is [imath]1.96[/imath].

When they tell you that [imath]95\%[/imath] of the area lies within [imath]1.96[/imath] standard deviation of the mean, they just mean the area under the curve is [imath]0.95[/imath] between [imath]-1.96[/imath] and [imath]1.96[/imath].

Or

[imath]\displaystyle P(-1.96 < X < 1.96) = \frac{1}{\sqrt{2\pi}}\int_{-1.96}^{1.96}e^{-\frac{x^2}{2}} \ dx \approx 0.95[/imath]

This result that I have just shown was the area for a [imath]95\%[/imath] confidence interval.

One last thing to mention is that:

If [imath]P(X < 1.96) = 0.975[/imath], it means [imath]P(X > 1.96) = P(X < -1.96) = 0.025[/imath] which is the area under each of the left and right tails.

The thing is by the empirical (68 - 95 - 99.7) rule, 95% of the area corresponds to a z score of 2, no? The z score of 1.96 corresponds to 95%. Isn't that confusing?
Can you clarify? Is this some kind of approximation?

 

[mario99]

The thing is by the empirical (68 - 95 - 99.7) rule, 95% of the area corresponds to a z score of 2, no? The z score of 1.96 corresponds to 95%. Isn't that confusing?
Can you clarify? Is this some kind of approximation?

Yes, it is just a fancy approximation. If you want to be so precise, even [imath]1.96[/imath] is wrong. What about [imath]1.95996398[/imath]? Do you want more digits or do you want to be fancy and just say [imath]2[/imath]?

 

[Dr.Peterson]

The thing is by the empirical (68 - 95 - 99.7) rule, 95% of the area corresponds to a z score of 2, no? The z score of 1.96 corresponds to 95%. Isn't that confusing?
Can you clarify? Is this some kind of approximation?

A full explanation of the empirical rule (as opposed to an introduction for students who may know nothing about the normal distribution yet) will say what is said here:

68–95–99.7 rule - Wikipedia

en.wikipedia.org

In statistics, the 68–95–99.7 rule, also known as the empirical rule, and sometimes abbreviated 3sr, is a shorthand used to remember the percentage of values that lie within an interval estimate in a normal distribution: approximately 68%, 95%, and 99.7% of the values lie within one, two, and three standard deviations of the mean, respectively.​

...​

​

It is just a memorable approximation, and should not be used if precision matters. If the probability you want is 95%, then z will not be exactly 2.

 

[Agent Smith]

Arigato gozaimus guys n gals, if any. @Dr.Peterson @mario99.