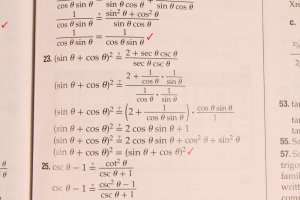jddoxtator
New member
- Joined
- May 28, 2024
- Messages
- 47
Wanted to thank you guys once again.
I have done more complex problems and a lot of them, and I am now able to simplify trigonometric identities in 4 to 5 lines instead of whole pages of circular logic, reliably.
I have done more complex problems and a lot of them, and I am now able to simplify trigonometric identities in 4 to 5 lines instead of whole pages of circular logic, reliably.