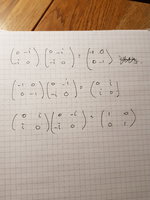I understand subgroups but I can't understand this question. I know that bc is the inverse, but I don't know the order the group to work out other subgroups. It says its less than 10, maybe that implies that the group is in fact of order 10. I know about La grange's theorem. So the inverse might be a group? I don't really understand why. Its the first question that I am having trouble with.
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
subgroups!
- Thread starter Sonal7
- Start date
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,986
It has been years since I worked with groups. I have not head-way with #1.I understand subgroups but I can't understand this question. I know that bc is the inverse, but I don't know the order the group to work out other subgroups. It says its less than 10, maybe that implies that the group is in fact of order 10. I know about La grange's theorem. So the inverse might be a group? I don't really understand why. Its the first question that I am having trouble with.]
Here is the basics for #2:
\(\displaystyle {\left( {\begin{array}{*{20}{c}} 0&i \\ i&0 \end{array}} \right)^2} = \left( {\begin{array}{*{20}{c}} { - 1}&0 \\ 0&{ - 1} \end{array}} \right)\)
\(\displaystyle {\left( {\begin{array}{*{20}{c}} 0&i \\ i&0 \end{array}} \right)^3} = \left( {\begin{array}{*{20}{c}} 0&{ - i} \\ { - i}&0 \end{array}} \right)\)
\(\displaystyle {\left( {\begin{array}{*{20}{c}} 0&i \\ i&0 \end{array}} \right)^4} = \left( {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right)\)
HERE is a useful link.
Last edited:
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,598
You say that you know about subgroups and then you say bc is the inverse. bc is the inverse of every element in the group? Or is bc the inverse of a or b or c? bc is the inverse of a single element of the subgroup! You need to make a Cayley table using what you know.I understand subgroups but I can't understand this question. I know that bc is the inverse, but I don't know the order the group to work out other subgroups. It says its less than 10, maybe that implies that the group is in fact of order 10. I know about La grange's theorem. So the inverse might be a group? I don't really understand why. Its the first question that I am having trouble with.
You know that the a*a=b, so put that in the table. You know that a^3=c, but a^3=a*a*a= a*(a*a) = a*b=c. Also a^3=a*a*a= (a*a)*a = b*a =c. Now a*b*c=(a*b)*c=c*c= a. Fill in the Cayley table as much as you can. Can you see an id element? Inverses for a, b and c? Do you need another element or 2 or 3....
Come on and show us some work. I assure you that the pieces will come together if you make the Cayley table!
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,986
Jomo. The real problem is that I see no way to conclude what the identity element is from the given.You say that you know about subgroups and then you say bc is the inverse. bc is the inverse of every element in the group? Or is bc the inverse of a or b or c? bc is the inverse of a single element of the subgroup!
Saying a term is "the inverse" means nothing if we do not know the identity.
I can show: \(\displaystyle c=ba=ab\), \(\displaystyle c^2=a\) but in additional of not knowing the identity what other elements can be in the group?
It can be shown that \(\displaystyle a^4=ca\) which leads to circular results.
So what happens if a new element say \(\displaystyle d\) is introduced?
I'm a beginner at this, I probably know less than anyone here including the OP ... but I know why he says that bc is the identity. We have abc = a, so by the associative property abc = a(bc) = a, which seems to imply that bc = e (where e is the identity, if that's the convention used in his text). If that's right, there should be an e in the Cayley table at the intersection of b and c. I haven't been able to fill out a workable Cayley table, though. I think there must be at least one more element, probably more.
@ pka ... I gather you disagree that bc = e. You are probably right, and I'm probably on the wrong track. Can you explain why bc is not = e?
@ pka ... I gather you disagree that bc = e. You are probably right, and I'm probably on the wrong track. Can you explain why bc is not = e?
HallsofIvy
Elite Member
- Joined
- Jan 27, 2012
- Messages
- 7,763
Do you have trouble with English? "Less than 10" is saying explicitly that it is NOT 10!It says its less than 10, maybe that implies that the group is in fact of order 10.
That doesn't even make sense! First there is no such thing as "the" inverse of a group. Every element of a group has its own inverse. Second, an inverse is a member of a group. It is not a "group" itself.I know about La grange's theorem. So the inverse might be a group?
You are told that "\(\displaystyle b= a^2\)", "\(\displaystyle c= a^3\)", and "\(\displaystyle abc= a\)". So \(\displaystyle a(a^2)(a^3)= a^6= a(a^5)= (a^5)a= a\). That tells you that \(\displaystyle a^5= e\), the group identity. And since \(\displaystyle bc= (a^2)(a^3)= a^5\), b and c are inverse to each other. Now, what are ab and ac and what is the inverse to a? This is basically a problem of determining what \(\displaystyle a^4\) is. Do you need to introduce a new member or can it be in terms of b and c?I don't really understand why. Its the first question that I am having trouble with.
yes I know it’s not 10. but the answer says that the order of the subgroup is 5. I thought that would only make sense if the Q implied that the order of the group is 10. I don’t know why it’s 5 , probably unrelated to the less than 10. Why have they said it’s less than 10? They may as well have said it’s less than 9. There must be an implied reason. lagranges theorem states something about inverses, I shall copy that in.Do you have trouble with English? "Less than 10" is saying explicitly that it is NOT 10!
That doesn't even make sense! First there is no such thing as "the" inverse of a group. Every element of a group has its own inverse. Second, an inverse is a member of a group. It is not a "group" itself.
You are told that "\(\displaystyle b= a^2\)", "\(\displaystyle c= a^3\)", and "\(\displaystyle abc= a\)". So \(\displaystyle a(a^2)(a^3)= a^6= a(a^5)= (a^5)a= a\). That tells you that \(\displaystyle a^5= e\), the group identity. And since \(\displaystyle bc= (a^2)(a^3)= a^5\), b and c are inverse to each other. Now, what are ab and ac and what is the inverse to a? This is basically a problem of determining what \(\displaystyle a^4\) is. Do you need to introduce a new member or can it be in terms of b and c?
5 is a factor of 10, and it’s the order of the subgroup. I m trying to copy it in.Do you have trouble with English? "Less than 10" is saying explicitly that it is NOT 10!
That doesn't even make sense! First there is no such thing as "the" inverse of a group. Every element of a group has its own inverse. Second, an inverse is a member of a group. It is not a "group" itself.
You are told that "\(\displaystyle b= a^2\)", "\(\displaystyle c= a^3\)", and "\(\displaystyle abc= a\)". So \(\displaystyle a(a^2)(a^3)= a^6= a(a^5)= (a^5)a= a\). That tells you that \(\displaystyle a^5= e\), the group identity. And since \(\displaystyle bc= (a^2)(a^3)= a^5\), b and c are inverse to each other. Now, what are ab and ac and what is the inverse to a? This is basically a problem of determining what \(\displaystyle a^4\) is. Do you need to introduce a new member or can it be in terms of b and c?
Lagrange’s theorem
When finding subgroups, Lagrange’s theorem, which states that the order of a subgroup of a finite group G is a factor of the order of G, can be very useful as it gives an idea of what order of subgroups you can look for.
It also tells you that all groups of prime order are cyclic.
If you need to find out whether or not a particular subset of a group forms a subgroup, or to show that a particular subset of a group is a subgroup, this is quite straightforward: all you have to do is to check the group axioms for the subset you are looking at.
If you want to find all the subgroups of a particular group, it is usually quite easy to find some, but it can be difficult to be sure whether you have found them all.
Remember in particular:
o By Lagrange’s theorem, the order of a subgroup must be a factor of the order of the group. So for a subgroup of order 8, look for subgroups of order 2 and 4 (in addition to the trivial subgroup and the group itself).
o Any self-inverse element forms a subgroup of order 2 with the identity element.
o When looking for subgroups of order 4, there are only two possible types of group of order 4. One type consists of the identity element and three other self-inverse elements, the other is the identity element, one other self-inverse element and an inverse pair.
When finding subgroups, Lagrange’s theorem, which states that the order of a subgroup of a finite group G is a factor of the order of G, can be very useful as it gives an idea of what order of subgroups you can look for.
It also tells you that all groups of prime order are cyclic.
If you need to find out whether or not a particular subset of a group forms a subgroup, or to show that a particular subset of a group is a subgroup, this is quite straightforward: all you have to do is to check the group axioms for the subset you are looking at.
If you want to find all the subgroups of a particular group, it is usually quite easy to find some, but it can be difficult to be sure whether you have found them all.
Remember in particular:
o By Lagrange’s theorem, the order of a subgroup must be a factor of the order of the group. So for a subgroup of order 8, look for subgroups of order 2 and 4 (in addition to the trivial subgroup and the group itself).
o Any self-inverse element forms a subgroup of order 2 with the identity element.
o When looking for subgroups of order 4, there are only two possible types of group of order 4. One type consists of the identity element and three other self-inverse elements, the other is the identity element, one other self-inverse element and an inverse pair.
There’s a Harvard lecture on inverses and subgroups. I will find it lateryes I know it’s not 10. but the answer says that the order of the subgroup is 5. I thought that would only make sense if the Q implied that the order of the group is 10. I don’t know why it’s 5 , probably unrelated to the less than 10. Why have they said it’s less than 10? They may as well have said it’s less than 9. There must be an implied reason. lagranges theorem states something about inverses, I shall copy that in.
1. “The first two equations imply that a 5 bc while the third implies that bc is the identity. Hence a has order 5. The order of the group must be a multiple of the order of any element and since we are told the order of the group is less than 10 this means the groupmusthaveorder5” I have copied the answer to Q1. I guess the choice of less than 10 was deliberate as you might argue it’s 10, 15, ... and other factors of 5. 5 is a prime number so it’s the subgroup required.Do you have trouble with English? "Less than 10" is saying explicitly that it is NOT 10!
That doesn't even make sense! First there is no such thing as "the" inverse of a group. Every element of a group has its own inverse. Second, an inverse is a member of a group. It is not a "group" itself.
You are told that "\(\displaystyle b= a^2\)", "\(\displaystyle c= a^3\)", and "\(\displaystyle abc= a\)". So \(\displaystyle a(a^2)(a^3)= a^6= a(a^5)= (a^5)a= a\). That tells you that \(\displaystyle a^5= e\), the group identity. And since \(\displaystyle bc= (a^2)(a^3)= a^5\), b and c are inverse to each other. Now, what are ab and ac and what is the inverse to a? This is basically a problem of determining what \(\displaystyle a^4\) is. Do you need to introduce a new member or can it be in terms of b and c?
Last edited:
That’s an easy question about why he stopped after the matrix was raised to the power 4 as he got to the identity element. He has generated all the elements of the group.You say that you know about subgroups and then you say bc is the inverse. bc is the inverse of every element in the group? Or is bc the inverse of a or b or c? bc is the inverse of a single element of the subgroup! You need to make a Cayley table using what you know.
You know that the a*a=b, so put that in the table. You know that a^3=c, but a^3=a*a*a= a*(a*a) = a*b=c. Also a^3=a*a*a= (a*a)*a = b*a =c. Now a*b*c=(a*b)*c=c*c= a. Fill in the Cayley table as much as you can. Can you see an id element? Inverses for a, b and c? Do you need another element or 2 or 3....
Come on and show us some work. I assure you that the pieces will come together if you make the Cayley table!
This has solved my problem a raised to the power 5 is the identity. So the order of the group is 5. I caused confusion by calling it a subgroup, I meant it’s the group.I'm a beginner at this, I probably know less than anyone here including the OP ... but I know why he says that bc is the identity. We have abc = a, so by the associative property abc = a(bc) = a, which seems to imply that bc = e (where e is the identity, if that's the convention used in his text). If that's right, there should be an e in the Cayley table at the intersection of b and c. I haven't been able to fill out a workable Cayley table, though. I think there must be at least one more element, probably more.
@ pka ... I gather you disagree that bc = e. You are probably right, and I'm probably on the wrong track. Can you explain why bc is not = e?
It has been years since I worked with groups. I have not head-way with #1.
Here is the basics for #2:
\(\displaystyle {\left( {\begin{array}{*{20}{c}} 0&i \\ i&0 \end{array}} \right)^2} = \left( {\begin{array}{*{20}{c}} { - 1}&0 \\ 0&{ - 1} \end{array}} \right)\)
\(\displaystyle {\left( {\begin{array}{*{20}{c}} 0&i \\ i&0 \end{array}} \right)^3} = \left( {\begin{array}{*{20}{c}} 0&{ - i} \\ { - i}&0 \end{array}} \right)\)
\(\displaystyle {\left( {\begin{array}{*{20}{c}} 0&i \\ i&0 \end{array}} \right)^4} = \left( {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right)\)
HERE is a useful link.
I have a problem with part 2 of the question. I dont understand how the answer is derived.
the other generator of G is the matrix:
(0, -i)
(-i,0)
This clearly wrong. Here is my working and it does not generate all the elements of the the group G! Its power of 2 just gives the identity. I might be wrong but I cant see where I have gone wrong.
Nope! I made a mistake, it is a generator of G!
Attachments
Last edited:
@sonal 7 ... I gather you've solved these two problems. I'm attaching my solution. I hope you can tell me whether it agrees with yours.
For Part 1, I don't think you need LaGrange's Theorem, but it's most helpful if you know that every cyclic group is abelian.
For Part 2, LaGrange's Theorem would be helpful, but I'm not sure it's really necessary.
You seem to be at the stage of development where the LaGrange Theorem seems almost magical. I only just got past that myself.
A question ... does your course include Cayley Diagrams, or only Cayley Tables? A lot or Abstract Algebra courses skip the Cayley Diagrams, which I think is a mistake. It helps to think of group in two ways, one as a collection of elements, and the other as a collection of actions. The Cayley Diagrams will help you with the second way. When you find a coset, that's like starting an orbit from a different place.
Here's a link to a youtube video. It helped me and it might help you:
Good luck. R
For Part 1, I don't think you need LaGrange's Theorem, but it's most helpful if you know that every cyclic group is abelian.
For Part 2, LaGrange's Theorem would be helpful, but I'm not sure it's really necessary.
You seem to be at the stage of development where the LaGrange Theorem seems almost magical. I only just got past that myself.
A question ... does your course include Cayley Diagrams, or only Cayley Tables? A lot or Abstract Algebra courses skip the Cayley Diagrams, which I think is a mistake. It helps to think of group in two ways, one as a collection of elements, and the other as a collection of actions. The Cayley Diagrams will help you with the second way. When you find a coset, that's like starting an orbit from a different place.
Here's a link to a youtube video. It helped me and it might help you:
Good luck. R
Attachments
Hi
I dont know much about group theory. Just bought some books on abstract algebra to try to get a deeper understanding. I know all the definitions such as what a cyclic group is, a generator is and how to draw a cayley diagram but not much clue about the deeper understanding of the topic. Its like when teachers taught me matrix multiplication and one thinks why would you do it like that ? Its when you see the connection with simultaneous equation, and actually that's why it was invented that things seem clearer. Why does the Lagranges theorem work? I am reasearching that. The books I am reading are good but it might take me a while to get there. I will start looking at the resources you posted a bit later on. Thanks
I dont know much about group theory. Just bought some books on abstract algebra to try to get a deeper understanding. I know all the definitions such as what a cyclic group is, a generator is and how to draw a cayley diagram but not much clue about the deeper understanding of the topic. Its like when teachers taught me matrix multiplication and one thinks why would you do it like that ? Its when you see the connection with simultaneous equation, and actually that's why it was invented that things seem clearer. Why does the Lagranges theorem work? I am reasearching that. The books I am reading are good but it might take me a while to get there. I will start looking at the resources you posted a bit later on. Thanks
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,986
You must learn to use the resources available to you.Why does the Lagranges theorem work? I am reasearching that. The books I am reading are good but it might take me a while to get there. I will start looking at the resources you posted a bit later on.
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,598
Some of you are talking about LaGrange's but this will not help as we do not know the order of the group other than it is less than 5. Sure 5 divides 10 but why would you say that as it has as much meaning as 6 divides 12 in this context.
Yes, bc=e-so we have a 4th element in this group as none of a, b and qualifies to be e. Know get your hands dirty, add e to the cayley table, update the table and see if these 4 elements can form a group. If not, then add a fifth element. Nobody knows everything but you must at least try. It is a puzzle that can be done by a 5th grader so just try. I guarantee you that you will be able to do it.
Yes, bc=e-so we have a 4th element in this group as none of a, b and qualifies to be e. Know get your hands dirty, add e to the cayley table, update the table and see if these 4 elements can form a group. If not, then add a fifth element. Nobody knows everything but you must at least try. It is a puzzle that can be done by a 5th grader so just try. I guarantee you that you will be able to do it.
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,986
I can show that this is a trick question Lets call \(\displaystyle P\) the superstition that \(\displaystyle a(bc)=a\).Some of you are talking about LaGrange's but this will not help as we do not know the order of the group other than it is less than 5.
So we accept both \(\displaystyle a^2=b~\&~a^3=c\) as true in the following two Cayley tables:
Table I \(\displaystyle \begin{array}{*{20}{c}}
\circ &|&e&a&b&c&d \\
\hline
e&|&e&a&b&c&d \\
a&|&a&b&c&d&e \\
b&|&b&c&d&e&a \\
c&|&c&d&e&a&b \\
d&|&d&e&a&b&c \end{array}\) TABLE II \(\displaystyle \begin{array}{*{20}{c}}
\circ &|&e&a&b&c \\ \hline
e&|&e&a&b&c \\
a&|&a&b&c&e \\
b&|&b&c&e&a \\
c&|&c&e&a&b \end{array}\)
Both of the tables conform to the accepted two conditions, but only table I conforms to the other condition \(\displaystyle P:~a(bc)=a\).
Note that both tables represent a group generated by \(\displaystyle a\)
In order to accomplish that we had to introduce an element \(\displaystyle d\). Now the group is order five and each non-rival element is order five.