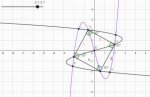
square on a cubic: Find k so square has 4 corners on y = x3 − kx

[Denis]

I tried letting u = x^2.....

Thanks for choosing "u"

 

[Dr.Peterson]

Still struggling on this...I tried letting u= x^2, reducing to a quartic and then thinking about (u^2+au+b)(u^2+cu+d) and trying to compare coefficients but that doesn't go anywhere nice!

I haven't done any more work on it. I did at one point find what may be your source for it, and it wasn't clear whether he would ever give an answer, or even had one. Do you have reason to expect either an exact or approximate answer found logically? What is your source?

But it's worth keeping in mind that we don't necessarily have to solve the equation for x; we just have to find conditions under which it has a solution. That may possibly be easier.

 

[apple2357]

I haven't done any more work on it. I did at one point find what may be your source for it, and it wasn't clear whether he would ever give an answer, or even had one. Do you have reason to expect either an exact or approximate answer found logically? What is your source?

But it's worth keeping in mind that we don't necessarily have to solve the equation for x; we just have to find conditions under which it has a solution. That may possibly be easier.

A friends son who is at university mentioned this problem to him and it was passed to me. I have no idea whether there is an exact answer but neither had solved it and but seemed to imply there was a neat value for minimum k, or so they were told! I might go back to them!

 

[apple2357]

Can you tell me if this makes sense?

So thinking about

x⁸-3kx⁶+3k²x⁴-(k³+k)x²+ k²​+1=0 (*)

In order for this to have 4 repeated roots it must be expressible in the form:

(x²-p²)²(x²-q²)²

Expanding this and comparing coefficients with (*)

We get

-2p²-2q²=-3k

q⁴+4p²q²+p⁴= 3k²

-2p²q⁴-2p⁴q²= -k³-k

p⁴q⁴=k²-1


Solving for k, i get k²= 8

So k= sqrt(8) is the critical value

 

[apple2357]

This is the root 8 case, Is this the minimum value or the only value?

 

[Dr.Peterson]

Can you tell me if this makes sense?

So thinking about

x⁸-3kx⁶+3k²x⁴-(k³+k)x²+ k²​+1=0 (*)

In order for this to have 4 repeated roots it must be expressible in the form:

(x²-p²)²(x²-q²)²

Expanding this and comparing coefficients with (*)

We get

-2p²-2q²=-3k

q⁴+4p²q²+p⁴= 3k²

-2p²q⁴-2p⁴q²= -k³-k

p⁴q⁴=k²-1


Solving for k, i get k²= 8

So k= sqrt(8) is the critical value

Great work; I think you've done it. Your answer agrees with my experimental 2.84 (which I mistyped at least once as 1.84). Now you've explained why you wrote the factors in that form previously, which I didn't recognize as useful.

I had considered looking for this 4-root case, but neglected to take this approach. I'll take the excuse that my main goal was to give you a chance to work it out yourself, so I didn't try too hard ...

 

[apple2357]

sqrt 8 is the minimum value:

 

[apple2357]

Great work; I think you've done it. Your answer agrees with my experimental 2.84 (which I mistyped at least once as 1.84). Now you've explained why you wrote the factors in that form previously, which I didn't recognize as useful.

I had considered looking for this 4-root case, but neglected to take this approach. I'll take the excuse that my main goal was to give you a chance to work it out yourself, so I didn't try too hard ...

Thanks. I nearly gave up on it 4 times...