Find their respective speeds

Oh, I think I should have drawn two points. One for each car, right?. Because both were at 40 kilos apart.
 
Let's see now
 

Attachments

  • paint_25-12-2020-04-11-32.jpg
    paint_25-12-2020-04-11-32.jpg
    187.5 KB · Views: 2
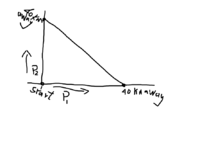
It looks to me that if I draw a line to join the two points at the 40 kms, a right triangle is formed. Just saying.
 
Hey, Khan said: Get the hypothenuse, the hypothenuse is 40, but I know the formula for the hypothenuse, and is not s=d/t .
Do I find the hypothenuse or do I go with the speed formula, what is the best way?.
 
Oh, I am sorry, first the hypothenuse and then the speed formula. Okay. Sorry.
 
eddy2017 said:
Hey, Khan said: Get the hypothenuse, the hypothenuse is 40, but I know the formula for the hypothenuse, and is not s=d/t .
Do I find the hypothenuse or do I go with the speed formula, what is the best way?.
Click to expand...
Go where? You have the right triangle which gives you a certain relationship that connects its sides. You have d=st. Any ideas?
 
I am stuck here. Don't know what to do next.
 

Attachments

  • 2020_12_25_0vh_Kleki.png
    2020_12_25_0vh_Kleki.png
    37.2 KB · Views: 3
Use the notation to help you.

You know the general formula relating average rate, distance, and time

[MATH]d = r * t.[/MATH]
Subhotosh Khan told you to label the unknowns.

[MATH]d_1 = \text {distance travelled by car 1.}[/MATH]
[MATH]r_1 = \text {average rate of car 1.}[/MATH]
[MATH]t_1 = \text {time traveled by car 1.}[/MATH]
[MATH]d_2= \text {distance travelled by car 2.}[/MATH]
[MATH]r_2 = \text {average rate of car 2.}[/MATH]
[MATH]t_2 = \text {time traveled by car 2.}[/MATH]
[MATH]x = \text {final distance between the cars.}[/MATH]
Are all of those unknown?

No. We know that [MATH]t_1 = 2 \text { and } t_2 = 2.[/MATH]
We also know that x = 40.

So there are four unknowns. That means we need four equations.

[MATH]2r_1 = d_1.[/MATH] Just applying the general rule to the specific case.

[MATH]2r_2 = d_2.[/MATH] Same thing.

And the problem tells you that [MATH]r_1 = r_2 + 4.[/MATH]
All of that should be almost automatic if you name the relevant variables, determine which are unknown, and look for the obvious equations. Now we need to determine the non-obvious equation or equations. We have found three and need four. That last equation is best found using a diagram and seeing that the Pythagorean Theorem applies.

What is that fourth equation? Once you have that, the thinking is over. It’s just manipulation of symbols after that.[/MATH]
 
Wow!. Well, I have to take my time, guys. I take my hat off to you all. Wow!. Ill get back to you. I'll have dinner now. Thanks a lot. I will rest a bit after dinner, reflect on what you have told me and be back early tomorrow again. Merry Christmas.
 
JeffM said:
Use the notation to help you.

You know the general formula relating average rate, distance, and time

[MATH]d = r * t.[/MATH]
Subhotosh Khan told you to label the unknowns.

[MATH]d_1 = \text {distance travelled by car 1.}[/MATH]
[MATH]r_1 = \text {average rate of car 1.}[/MATH]
[MATH]t_1 = \text {time traveled by car 1.}[/MATH]
[MATH]d_2= \text {distance travelled by car 2.}[/MATH]
[MATH]r_2 = \text {average rate of car 2.}[/MATH]
[MATH]t_2 = \text {time traveled by car 2.}[/MATH]
[MATH]x = \text {final distance between the cars.}[/MATH]
Are all of those unknown?

No. We know that [MATH]t_1 = 2 \text { and } t_2 = 2.[/MATH]
We also know that x = 40.

So there are four unknowns. That means we need four equations.

[MATH]2r_1 = d_1.[/MATH] Just applying the general rule to the specific case.

[MATH]2r_2 = d_2.[/MATH] Same thing.

And the problem tells you that [MATH]r_1 = r_2 + 4.[/MATH]
All of that should be almost automatic if you name the relevant variables, determine which are unknown, and look for the obvious equations. Now we need to determine the non-obvious equation or equations. We have found three and need four. That last equation is best found using a diagram and seeing that the Pythagorean Theorem applies.

What is that fourth equation? Once you have that, the thinking is over. It’s just manipulation of symbols after that.[/MATH]
Click to expand...
Thanks,
I am writing it out on paper.
I have a question.
Why do you say that
t1=2
and
t2=2

How do we know that?.
.
 
Last edited:
You must log in or register to reply here.
Top