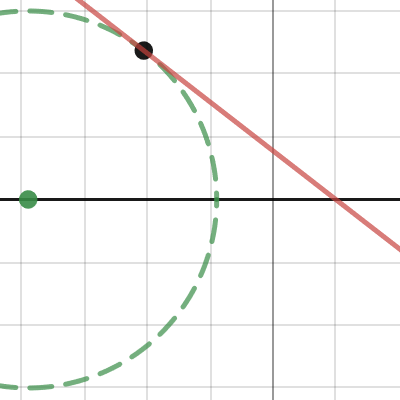
Meanwhile still trying to understand the statement you made :
“ B continuing along the straight line trajectory until reaching the line y=6.”
I guess you mean B traveling in a slope till a distance of 6 , probably with an angle of 60 degree making an equilateral triangle with its initial position and A . I tried that but kind of stuck there .
“ B continuing along the straight line trajectory until reaching the line y=6.”
I guess you mean B traveling in a slope till a distance of 6 , probably with an angle of 60 degree making an equilateral triangle with its initial position and A . I tried that but kind of stuck there .
Last edited: