Problem.
Express cos(2α) and sin(2α) in terms of sin(α) if 23π≤α≤25π.
Here's my attempt at solving this problem. Could someone please review my reasoning and let me know if it's correct?
sin(α)=2sin(2α)cos(2α)sin2(2α)+cos2(2α)=1
By addition and subtraction of the above identities we obtain
sin(2α)+cos(2α)=±1+sin(α)sin(2α)−cos(2α)=±1−sin(α)
Adding and subtracting again, we have
2sin(2α)=±1+sin(α)±1−sin(α)2cos(2α)=±1+sin(α)∓1−sin(α)
Since
sin(2α)+cos(2α)=2(21sin(α)+21cos(α))=2sin(2α+4π)
The expression is positive if
2kπ−4π<2α<2kπ+43π
Similarly
sin(2α)−cos(2α)=2(21sin(α)−21cos(α))=2sin(2α−4π)
And this positive if
2kπ+4π<2α<2kπ+45π
And negative otherwise.
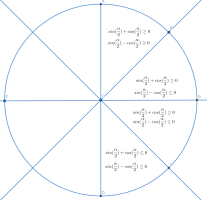
The condition for α as 23π≤α≤25π can be rewritten as 2−π≤α≤2π. We can now draw the possible cases on a circle.
Case (1): For 2−π≤α≤4−π
sin(2α)+cos(2α)≤0sin(2α)−cos(2α)≤0.
Therefore
sin(2α)=−21(1+sin(α)+1−sin(α))cos(2α)=−21(1+sin(α)−1−sin(α))
Case (2): For 4−π≤α≤4π
sin(2α)+cos(2α)≥0sin(2α)−cos(2α)≤0.
Thus
sin(2α)=21(1+sin(α)−1−sin(α))cos(2α)=21(1+sin(α)+1−sin(α))
Case (3): For 4π≤α≤2π
sin(2α)+cos(2α)≥0sin(2α)−cos(2α)≥0.
Therefore
sin(2α)=21(1+sin(α)+1−sin(α)) cos(2α)=21(1+sin(α)−1−sin(α))
Express cos(2α) and sin(2α) in terms of sin(α) if 23π≤α≤25π.
Here's my attempt at solving this problem. Could someone please review my reasoning and let me know if it's correct?
sin(α)=2sin(2α)cos(2α)sin2(2α)+cos2(2α)=1
By addition and subtraction of the above identities we obtain
sin(2α)+cos(2α)=±1+sin(α)sin(2α)−cos(2α)=±1−sin(α)
Adding and subtracting again, we have
2sin(2α)=±1+sin(α)±1−sin(α)2cos(2α)=±1+sin(α)∓1−sin(α)
Since
sin(2α)+cos(2α)=2(21sin(α)+21cos(α))=2sin(2α+4π)
The expression is positive if
2kπ−4π<2α<2kπ+43π
Similarly
sin(2α)−cos(2α)=2(21sin(α)−21cos(α))=2sin(2α−4π)
And this positive if
2kπ+4π<2α<2kπ+45π
And negative otherwise.
The condition for α as 23π≤α≤25π can be rewritten as 2−π≤α≤2π. We can now draw the possible cases on a circle.
Case (1): For 2−π≤α≤4−π
sin(2α)+cos(2α)≤0sin(2α)−cos(2α)≤0.
Therefore
sin(2α)=−21(1+sin(α)+1−sin(α))cos(2α)=−21(1+sin(α)−1−sin(α))
Case (2): For 4−π≤α≤4π
sin(2α)+cos(2α)≥0sin(2α)−cos(2α)≤0.
Thus
sin(2α)=21(1+sin(α)−1−sin(α))cos(2α)=21(1+sin(α)+1−sin(α))
Case (3): For 4π≤α≤2π
sin(2α)+cos(2α)≥0sin(2α)−cos(2α)≥0.
Therefore
sin(2α)=21(1+sin(α)+1−sin(α)) cos(2α)=21(1+sin(α)−1−sin(α))