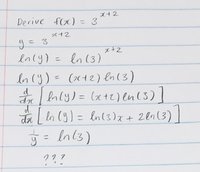Differentiating Exponential Functions

E

eutas1

Junior Member
Joined
Apr 8, 2021
Messages
165
How do you calculate the derivative of this without using first principles? I am not sure if I have learnt this or if I'm just being stupid and forgot how to do it...
Please refer to the attachment - I have included my working out using the general derivative method and chain rule.

Thank you!
 

Attachments

  • 1618236935198.png
    1618236935198.png
    47.4 KB · Views: 4
given [MATH]u[/MATH] as a differentiable function of [MATH]x[/MATH] and [MATH]a > 0[/MATH]
[MATH]\frac{d}{dx} (a^u) = a^u \cdot \ln(a) \cdot \frac{du}{dx}[/MATH]
try again

btw ...

note that [MATH]3^{x+2} = 3^2 \cdot 3^x[/MATH]
 
skeeter said:
given [MATH]u[/MATH] as a differentiable function of [MATH]x[/MATH] and [MATH]a > 0[/MATH]
[MATH]\frac{d}{dx} (a^u) = a^u \cdot \ln(a) \cdot \frac{du}{dx}[/MATH]
try again

btw ...

note that [MATH]3^{x+2} = 3^2 \cdot 3^x[/MATH]
Click to expand...

Oh, we actually did not learn that... Thank you for your help! :)
 
[MATH]y = a^u[/MATH]
[MATH]\ln{y} = \ln{a^u}[/MATH]
[MATH]\ln{y} = u \cdot \ln{a}[/MATH]
[MATH]\frac{d}{dx} \bigg[\ln{y} = u \cdot \ln{a} \bigg] [/MATH]
[MATH]\frac{1}{y} \cdot \frac{dy}{dx} = \ln{a} \cdot \frac{du}{dx}[/MATH]
[MATH]\frac{dy}{dx} = y \cdot \ln{a} \cdot \frac{du}{dx} = a^u \cdot \ln{a} \cdot \frac{du}{dx}[/MATH]
 
The rule you used is only when the base is x and the power is a real number. That is the derivative, for example, of x^3 is 3x^2. The derivative of 3^x is NOT x*3^(x-1) NO!
 
Dr.Peterson said:
If you don't know that formula, you can derive it by writing \(a^u = (e^{\ln a})^u = e^{u\ln a}\) and applying the chain rule.
Click to expand...

Oh yes, I did this afterwards and was able to do the entire question that this was extracted from.
Thank you!
 
skeeter said:
[MATH]y = a^u[/MATH]
[MATH]\ln{y} = \ln{a^u}[/MATH]
[MATH]\ln{y} = u \cdot \ln{a}[/MATH]
[MATH]\frac{d}{dx} \bigg[\ln{y} = u \cdot \ln{a} \bigg] [/MATH]
[MATH]\frac{1}{y} \cdot \frac{dy}{dx} = \ln{a} \cdot \frac{du}{dx}[/MATH]
[MATH]\frac{dy}{dx} = y \cdot \ln{a} \cdot \frac{du}{dx} = a^u \cdot \ln{a} \cdot \frac{du}{dx}[/MATH]
Click to expand...

I only understand up to this step:
1618303457263.png

I do not know how to derive ln(3) ...
 
Jomo said:
The rule you used is only when the base is x and the power is a real number. That is the derivative, for example, of x^3 is 3x^2. The derivative of 3^x is NOT x*3^(x-1) NO!
Click to expand...

Ah I see, thank you!
 
on the left side, the derivative of [MATH]\ln{y}[/MATH] is [MATH]\frac{1}{y} \cdot \frac{dy}{dx}[/MATH] because y is a function of x ... chain rule

to finish, multiply both sides by y, which is your original exponential function
 
skeeter said:
on the left side, the derivative of [MATH]\ln{y}[/MATH] is [MATH]\frac{1}{y} \cdot \frac{dy}{dx}[/MATH] because y is a function of x ... chain rule

to finish, multiply both sides by y, which is your original exponential function
Click to expand...

But then you would get:
1 = ln(3) * 3^(x+2) ?? Which is not the answer of ln(3) * 3^(x+2)
 
once again ...

the derivative of [MATH]\ln{y}[/MATH] is NOT [MATH]\frac{1}{y}[/MATH],

[MATH]\frac{d}{dx} \ln{y} = \frac{1}{y} \cdot \color{red} \frac{dy}{dx}[/MATH]
y is a function of x ... the chain rule applies here
 
skeeter said:
once again ...

the derivative of [MATH]\ln{y}[/MATH] is NOT [MATH]\frac{1}{y}[/MATH],

[MATH]\frac{d}{dx} \ln{y} = \frac{1}{y} \cdot \color{red} \frac{dy}{dx}[/MATH]
y is a function of x ... the chain rule applies here
Click to expand...

What is the answer for dy/dx ?
 
skeeter said:
[MATH]y = 3^{x+2}[/MATH]
[MATH]\frac{dy}{dx} = \ln{3} \cdot 3^{x+2}[/MATH]
see post #14 again ...
Click to expand...

But my whole issue was that I never learnt how to derive something where the base is a number...
 
You must log in or register to reply here.
Top