Okay. And I assume I'm right that what you want to count is the number of sets of up to 30 cups that can be arranged according to these rules.
Before we can find the probability of being able to arrange a random set, in addition to this count we will need to figure out the probability distribution of the sets of cups themselves. I've suggested that each of the (2+31)*30/2 = 495 possible sets in your list might be equally likely, making that your denominator; but I don't know that. How is a set of cups being formed? Are you randomly picking a number of cups to use, and then randomly picking out one cup at a time from a collection of 30 of each color? Or what? If this is a real-life question, that may turn out to be the hardest part.
But getting back to the counting, my next idea would be to make a big 31 by 31 grid, so that the nth cell in the mth row (each numbered from 0 through 30) represents a set with m gray and n yellow cups, and start marking cells as possible or not, and recording the reasons for each. Each case (like those in your earlier list) will let you fill in a lot of cells at once, and eventually you may have just a few left to figure out individually. This will go a lot faster than what you've been doing with your spreadsheet, even though it is essentially the same idea, because you can see everything at once and quickly fill in related cases. You may even find a bigger pattern that could make it possible to come up with a formula, though I doubt it.
(By the way, this grid would allow up to 60 cups, so all cells below a diagonal will be empty. Probably cell (0,0) would also be empty. This leaves 31*32/2 - 1 = 495 valid cells.)
By the way, I wonder if anyone can figure out why you would see your pictures in post #21 differently than I do? That may be a bug in the software.
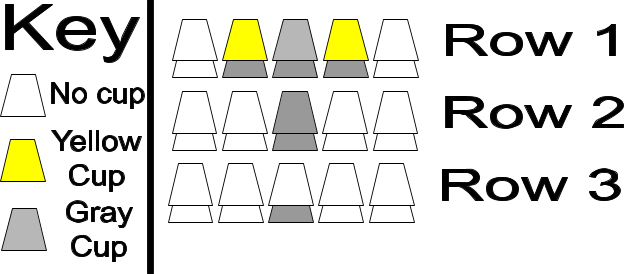

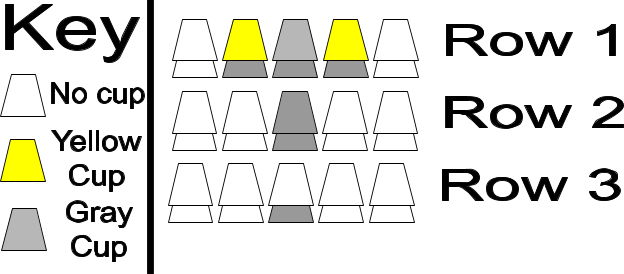
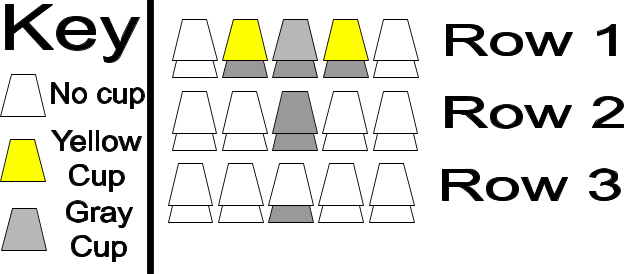


![20191231_085002[2].jpg 20191231_085002[2].jpg](https://www.freemathhelp.com/forum/data/attachments/13/13125-e4e057d38d2c57dc6e2c1acbc64be6e6.jpg)
![20191231_085007[2].jpg 20191231_085007[2].jpg](https://www.freemathhelp.com/forum/data/attachments/13/13126-996579ad82c66ccb8080663aae7c81c2.jpg)