logistic_guy
Full Member
- Joined
- Apr 17, 2024
- Messages
- 570
here is the question
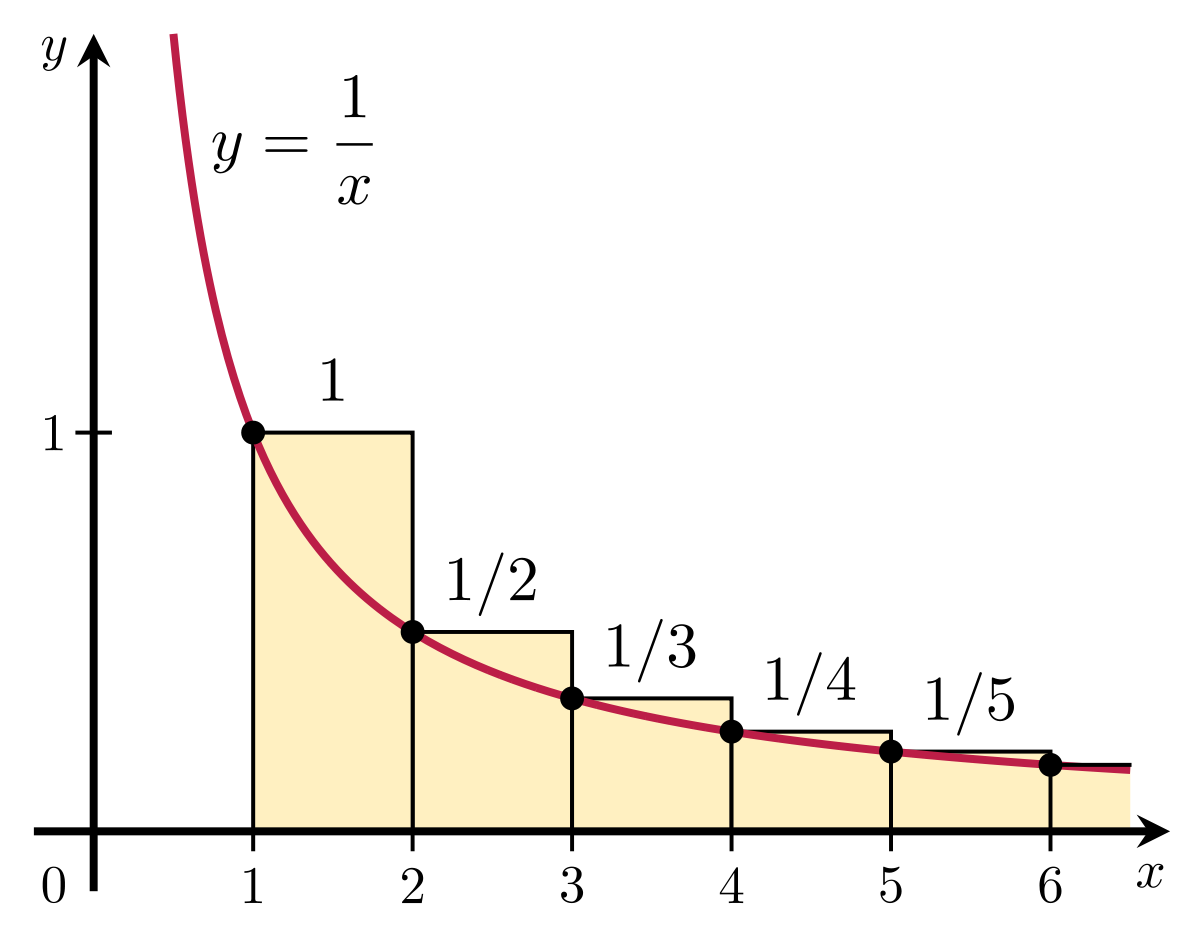
Does the infinite series \(\displaystyle \sum_{n=1}^{\infty}\frac{1}{n}\) converge or diverge?
my attemb
this series is famous for divergence
am i correct?
Does the infinite series \(\displaystyle \sum_{n=1}^{\infty}\frac{1}{n}\) converge or diverge?
my attemb
this series is famous for divergence
am i correct?