Scrutinize
Junior Member
- Joined
- Sep 16, 2019
- Messages
- 52
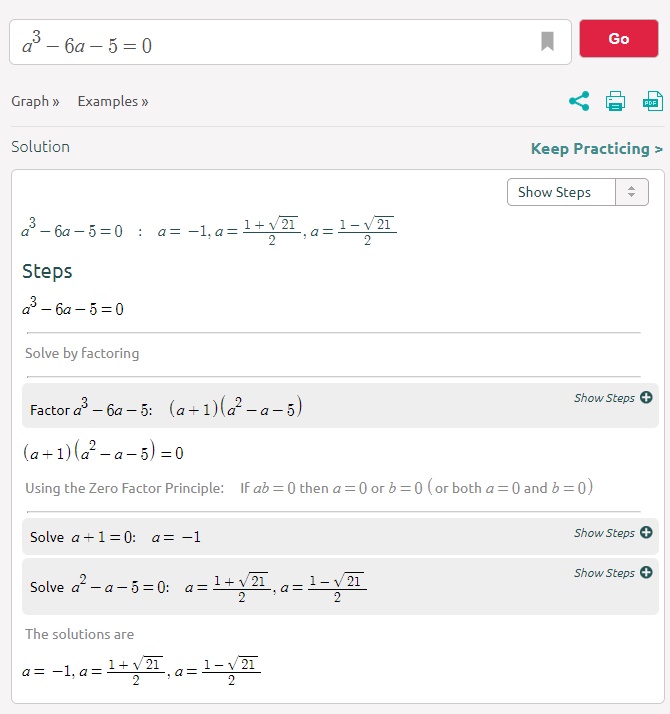
Yea but when I solve that equation I get the wrong answer? I got 1+ 21^(1/2) divided by two and the same but minus. And when I plugged the equation into a calculator it gave that answer too, which was wrong. Is there a small mistake that we're making maybe?
[MATH]0=\frac{4a+1}{(a^2-1)^{\frac{3}{2}}}(a+1)+\frac{a+4}{\sqrt{a^2-1}}[/MATH]
This is the exact equation I am using.
[MATH]0=\frac{4a+1}{(a^2-1)^{\frac{3}{2}}}(a+1)+\frac{a+4}{\sqrt{a^2-1}}[/MATH]
This is the exact equation I am using.