basic infinite series

[logistic_guy]

here is the question

Does the infinite series \(\displaystyle \sum_{n=1}^{\infty}\frac{1}{n}\) converge or diverge?


my attemb
this series is famous for divergence
am i correct?

 

[fresh_42]

Yes. Do you have an idea of how to prove it?

 

[logistic_guy]

thank

Yes.

the question don't ask to show if the series converge or diverge
don't this mean my answer is complete?

Do you have an idea of how to prove it?

i've not only idea but many ideas
i know there is some tests to use
the problem i'm still lack the skills of how to chose the correct test

if i randomly chose the comparison test
i know \(\displaystyle \frac{1}{n} > \frac{1}{n^2}\)
i also know \(\displaystyle \frac{1}{n^2}\) converge
i don't know how to use this idea to say \(\displaystyle \frac{1}{n}\) diverge

 

[fresh_42]

the question don't ask to show if the series converge or diverge
don't this mean my answer is complete?

I would say no since a mathematical answer without proof is problematic. It's not legal science or biology where facts are asked.

i've not only idea but many ideas
i know there is some tests to use
the problem i'm still lack the skills of how to chose the correct test

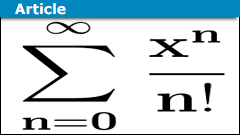
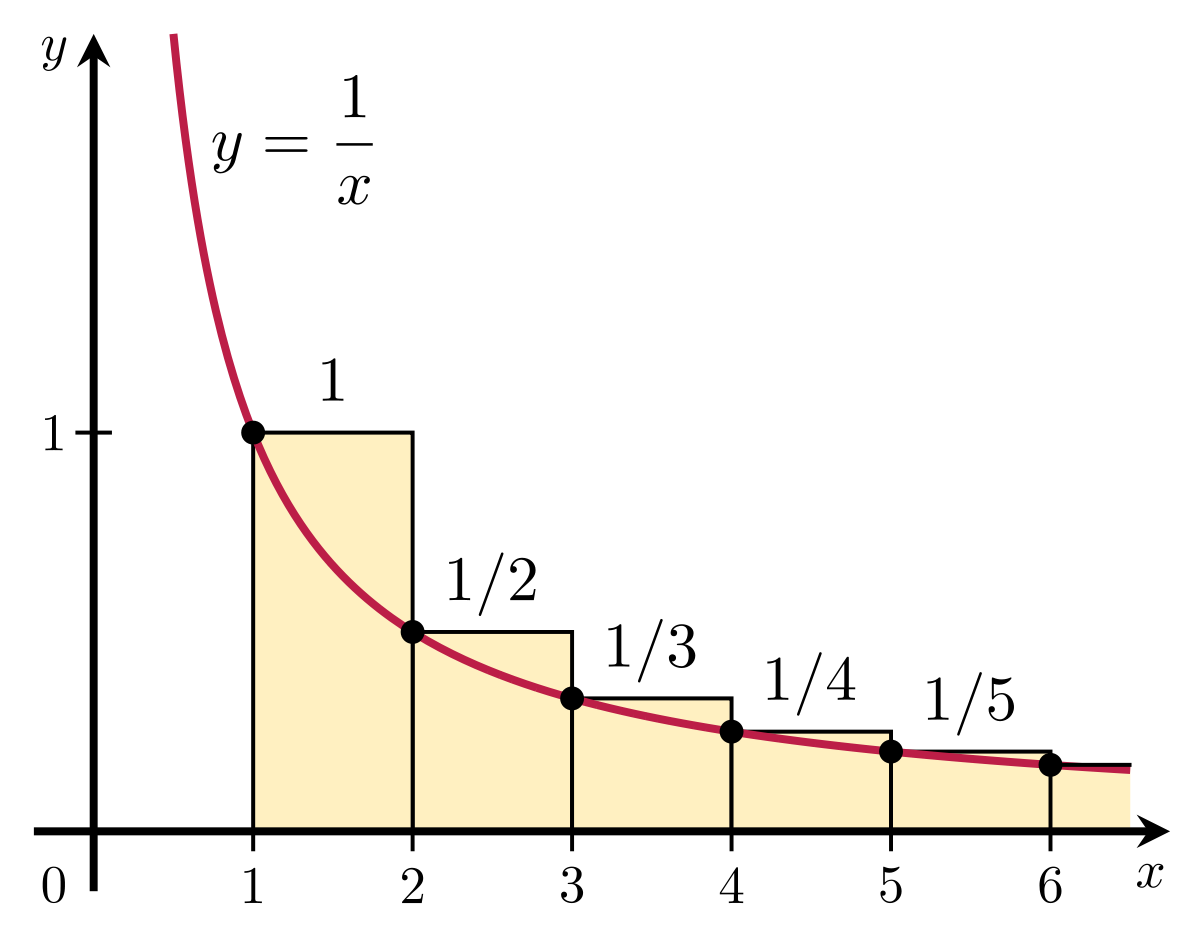
The oldest proof I've read about is from the 14th century! It is far easier than any criteria. We are asked about the value of
[math] 1+\dfrac{1}{2} + \dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\ldots [/math]and we can group the terms:
[math] 1+\dfrac{1}{2} + \left(\dfrac{1}{3}+\dfrac{1}{4}\right)+\left(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}\right)+\left(\dfrac{1}{9}+\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{16}\right)+\ldots [/math]Now every sum in the parentheses is greater than [imath] 1/2 [/imath] and thus they sum up to infinity.

All convergence criteria come down to a direct comparison test if you look at their proofs: find a convergent series that is greater to prove convergence and a divergent series that is less for divergence. Here is a little article about it:

Series in Mathematics: From Zeno to Quantum Theory

Explore the profound impact of series in mathematics, tracing their historical significance from ancient mathematicians to quantum theory.

www.physicsforums.com