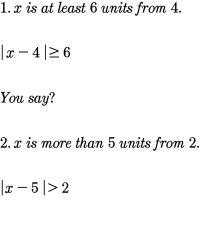Write Statements As Inequality

[mathdad]

See attachment.

Write statements as inequality.

 

[topsquark]

See attachment.

Write statements as inequality.

What are your attempts?

-Dan

 

[Dr.Peterson]

See attachment.

Write statements as inequality.

​

One of your answers is wrong.

 

[mathdad]

View attachment 38568​

One of your answers is wrong.

Which one is wrong? Why?

 

[Dr.Peterson]

Which one is wrong? Why?

That's for you to think about. Remember, we don't just give answers. We want to teach you to think, and sometimes the best way to do that is just to tell you to look again, which is how I catch my own errors. (I do that all the time in face-to-face tutoring.)

 

[mathdad]

That's for you to think about. Remember, we don't just give answers. We want to teach you to think, and sometimes the best way to do that is just to tell you to look again, which is how I catch my own errors. (I do that all the time in face-to-face tutoring.)

This statement tells me that the distance between a number ‘x’ and the number 2 is greater than 5 units. I can represent this with an inequality using absolute value this way:

|x - 2| > 5

I think this inequality has two possible solutions:

x > 7:

x is more than 5 units to the right of 2.

x < -3:

x is more than 5 units to the left of 2.

Am I right?

 

[Dr.Peterson]

This statement tells me that the distance between a number ‘x’ and the number 2 is greater than 5 units. I can represent this with an inequality using absolute value this way:

|x - 2| > 5

Good. You found the wrong one and corrected it.

I think this inequality has two possible solutions:

x > 7:

x is more than 5 units to the right of 2.

x < -3:

x is more than 5 units to the left of 2.

Rather than say "two possible solutions" (which made me think you were going to give just two specific numbers, I'd say there are two cases: Either the number is greater than 7 (more than 5 greater than 2), or it is less than -3 (more then 5 less than 2.

So you're correct.

It's very easy to quickly write something that is not what you intended (or should have intended). That's why I always look at what I wrote to see if it really answers the question.

 

[mathdad]

Good. You found the wrong one and corrected it.


Rather than say "two possible solutions" (which made me think you were going to give just two specific numbers, I'd say there are two cases: Either the number is greater than 7 (more than 5 greater than 2), or it is less than -3 (more then 5 less than 2.

So you're correct.

It's very easy to quickly write something that is not what you intended (or should have intended). That's why I always look at what I wrote to see if it really answers the question.

Thank you.