word problem with natural log...any help is appreciated

[ballet432]

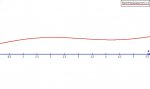
The profits of a company (billions) is given by P(t) = 4+ln(2sin(t)+t+1) over the time interval [0,2pi]
FIND:
a)exact coordinates of the absolute max and min.
b) find the ma rate of increase of profits and the min rate of decrease of profits to the nearest thousandth. (hint max p'(t) is when p''(t) = o or at the endpts.

I understand thatr you need to take the 1st and 2nd derivatives, but I am really confused on this problem. Thank you for your help!

 

[galactus]

The absolute max and min are the most extreme points over the interval, \(\displaystyle [0, \;\ 2\pi]\)

\(\displaystyle \frac{d}{dt}\left[4+ln(2sin(t)+t+1)\right]=\frac{2cos(t)+1}{2sin(t)+t+1}\)

Set the numerator to 0 and solve for t to find the max and min.

\(\displaystyle 2cos(t)+1=0\)

Solve for t:

\(\displaystyle \text{max t}=\frac{2\pi}{3}, \;\ \text{min t}=\frac{4\pi}{3}\)

To find the points of most increasing or decreasing, the second derivative will come in handy.

\(\displaystyle f''(x)=\frac{-4cos(t)-2(t+1)sin(t)-5}{(2sin(t)+t+1)^{2}}\)

Set to 0, solve for t, and the inflection points are at t=3.2626 and t=5.62

The inflection points are the points where the curve changes concavity. Thus, it is an extreme rate of increase or decrease.

The profit increases from 0 to \(\displaystyle \frac{2\pi}{3}\). Then, decreases down to \(\displaystyle \frac{4\pi}{3}\). Then, increases up to \(\displaystyle 2\pi\)

We can see this from the graph. If \(\displaystyle f''(x_{0})>0\), then we have a relative minimum.

At \(\displaystyle f''(\frac{2\pi}{3})=-.35588667..\)..........a maximum

At \(\displaystyle f''(\frac{4\pi}{3})=.501065...\)..............a minimum

Check the endpoints as well.

 

[ballet432]

find the max rate of increase of profits and the min rate of decrease of profits to the nearest thousandth. (hint max p'(t) is when p''(t) = o or at the endpts.

I'm still confused about this part
thanks for your help!

 

[Deleted member 4993]

find the max rate of increase of profits and the min rate of decrease of profits to the nearest thousandth. (hint max p'(t) is when p''(t) = o or at the endpts.

I'm still confused about this part
thanks for your help!

At what value of 't' - you have p'(t) maximum? - where do you have p"(t) =0?

Galactus gave you the answers above - read his post carefully!!!