I have been able to do a few word problems concerning change in rates and in two dimensions. I am having trouble with this problem in three dimensions.
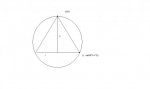
A right cone is inscribed in a sphere of radius a, find the maximum volume the cone can be in terms of radius a.
I know I can write x^2 + y^2 = a^2
And Volume of cone equals pi * r^2 * h.
I think the radius is x and the height is y+a but this yields an equation when differentiated makes no sense.
I need some kind of hint to help me get Volume of the Cone as a function of radius and then I can maximize the volume by differentiating.
Quite stuck, attempted many times.
A right cone is inscribed in a sphere of radius a, find the maximum volume the cone can be in terms of radius a.
I know I can write x^2 + y^2 = a^2
And Volume of cone equals pi * r^2 * h.
I think the radius is x and the height is y+a but this yields an equation when differentiated makes no sense.
I need some kind of hint to help me get Volume of the Cone as a function of radius and then I can maximize the volume by differentiating.
Quite stuck, attempted many times.