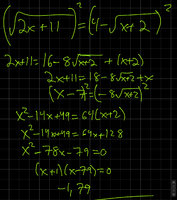I'm just checking to make sure I didn't misunderstand something
Question: Which step do you not need to do in this problem?
√(2x+11)=4-√(x+2)
a) Square both sides twice
b) Take the positive and negative square root
c) Factor
d) Check answers
e) Answer is not there
I have attached my work. You have to square both sides twice in the problem, and you also have to factor. The two solutions from factoring and setting the two binomials to 0 give you the solutions -1 and 79. You have to check the answers, because 79 is in fact not a solution, only -1 is. That is why my answer is B, since, in my solution, I did not take the positive and negative square root. Just double checking that I didn't overlook a step.
Question: Which step do you not need to do in this problem?
√(2x+11)=4-√(x+2)
a) Square both sides twice
b) Take the positive and negative square root
c) Factor
d) Check answers
e) Answer is not there
I have attached my work. You have to square both sides twice in the problem, and you also have to factor. The two solutions from factoring and setting the two binomials to 0 give you the solutions -1 and 79. You have to check the answers, because 79 is in fact not a solution, only -1 is. That is why my answer is B, since, in my solution, I did not take the positive and negative square root. Just double checking that I didn't overlook a step.