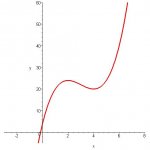
The Question:
1) f(x) = x[sup:30prntn5]3[/sup:30prntn5]-9x[sup:30prntn5]2[/sup:30prntn5]+24x+4
Find:
a) local extrema
b) Inflection Points
c.1) f(x) increasing
c.2) f(x) decreasing
d.1) concave up
d.2) concave down
My work:
y'= 3x[sup:30prntn5]2[/sup:30prntn5]-18x+24 OR (3x-12)(x-2)
y''=6x-18
a) Ran y' through quadratic equation, got 2,4. Graph confirms.
b)
6x-18=0
6x=18
x=3, Graph confirms.
c.1)
(3x-12)(x-2)>0
3x-12>0
3x>12 x>4, graph confirms.
x-2>0
x>2. Uh, what? That should be x<2.
c.2) Same as above, but reversed, getting x>2 (graph confirms) and x>4 (What?)
d.1)
6x-18>0
6x>18
x>3, graph confirms.
d.2)
6x-18<0
6x<18
x<3, graph confirms.
What am I screwing up on c.1 and c.2?
1) f(x) = x[sup:30prntn5]3[/sup:30prntn5]-9x[sup:30prntn5]2[/sup:30prntn5]+24x+4
Find:
a) local extrema
b) Inflection Points
c.1) f(x) increasing
c.2) f(x) decreasing
d.1) concave up
d.2) concave down
My work:
y'= 3x[sup:30prntn5]2[/sup:30prntn5]-18x+24 OR (3x-12)(x-2)
y''=6x-18
a) Ran y' through quadratic equation, got 2,4. Graph confirms.
b)
6x-18=0
6x=18
x=3, Graph confirms.
c.1)
(3x-12)(x-2)>0
3x-12>0
3x>12 x>4, graph confirms.
x-2>0
x>2. Uh, what? That should be x<2.
c.2) Same as above, but reversed, getting x>2 (graph confirms) and x>4 (What?)
d.1)
6x-18>0
6x>18
x>3, graph confirms.
d.2)
6x-18<0
6x<18
x<3, graph confirms.
What am I screwing up on c.1 and c.2?