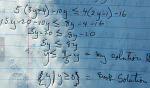allegansveritatem
Full Member
- Joined
- Jan 10, 2018
- Messages
- 962
Here is the problem:
13. Solve \(\displaystyle 5\, (3y\, -\, 4)\, -\, 10y\, \leq\, 4\, (2y\, -\, 1)\, -\, 16\)
Here is what I did with it:
. . . . .\(\displaystyle 5\, (3y\, -\, 4)\, -\, 10y\, \leq\, 4\, (2y\, -\, 1)\, -\, 16\)
. . . . .\(\displaystyle 15y\, -\, 20\, -\, 10y\, \leq\, 8y\, -\, 4\, -\, 16\)
. . . . .\(\displaystyle 5y\, -\, 20\, \leq\, 8y\, -\, 20\)
. . . . .\(\displaystyle 5y\, \leq\, 8y\)
. . . . .\(\displaystyle y\, \leq\, \dfrac{8}{5}\, y\)
My question is: Is my work correct? And if so, did I carry it far enough? If not, how to carry it further. Or, is my work correct but the book answer simply states my solution in another form?
13. Solve \(\displaystyle 5\, (3y\, -\, 4)\, -\, 10y\, \leq\, 4\, (2y\, -\, 1)\, -\, 16\)
Here is what I did with it:
. . . . .\(\displaystyle 5\, (3y\, -\, 4)\, -\, 10y\, \leq\, 4\, (2y\, -\, 1)\, -\, 16\)
. . . . .\(\displaystyle 15y\, -\, 20\, -\, 10y\, \leq\, 8y\, -\, 4\, -\, 16\)
. . . . .\(\displaystyle 5y\, -\, 20\, \leq\, 8y\, -\, 20\)
. . . . .\(\displaystyle 5y\, \leq\, 8y\)
. . . . .\(\displaystyle y\, \leq\, \dfrac{8}{5}\, y\)
My question is: Is my work correct? And if so, did I carry it far enough? If not, how to carry it further. Or, is my work correct but the book answer simply states my solution in another form?
Attachments
Last edited by a moderator: