What is the probability that they will meet if..

[Guest]

hello again,

A network of city streets forms square bloacks as shown in the diagram.

>

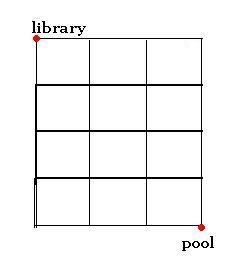Jeanine leaves the library and walks toward the pool at the same time as Miguel leaves the pools and walks toward the lbrary. Neither person follows a particular route, except that both are always moving toward their destination. What is the probability that they will meet if they both walk at the same rate?

How would I start this type of question, I havn't approached this ind of grid square question yet.. so I have no idea how to begin

thanks

 

[pka]

Look at my revised diagram. The key to this problem is the phrase “they both walk at the same rate” Hence they meet only after walking three and one-half blocks. Therefore if they meet it will be at one of the seven points A to G.

If Jeanine leaves the library and walks to the pool, she will have gone south four blocks and east three blocks. The number of ways she can do that is the number of ways to rearrange the string “SSSSEEE” which is \(\displaystyle \frac{{7!}}{{\left( {4!} \right)\left( {3!} \right)}}.\) That is the same number of ways Miguel goes from the pools to the library. What is the probability that they take exactly the same path?

BUT they do not have to take the same path in order to meet.
For them to meet at A or G each must take the same path. WHY?

For them to meet at B there is only one path for Jeanine but three paths for Miguel. WHY?

Now you must do this for C, D only. WHY?