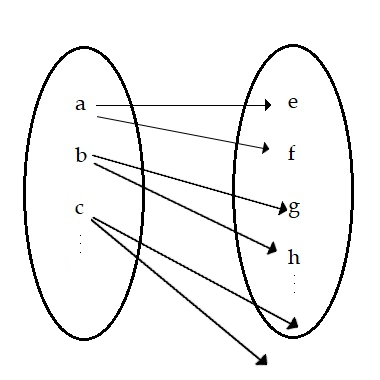
All I've ever seen is how to determine if something is a function or not. A vertical parabola is a function. But what set of relations do sideways parabolas fall in? To be precise, what do we call a relation that has two y outputs for every one x input, rather than being one-to-one like a function? Is there a term, or do we just say, "Not-a-function?" Is it just called a "one-to-many" relation?
I don't recall ever going over this in any math class I took. If we did, it was probably five minutes. So, thanks for any info on the term to describe things like [imath]y^2 = x[/imath].
I don't recall ever going over this in any math class I took. If we did, it was probably five minutes. So, thanks for any info on the term to describe things like [imath]y^2 = x[/imath].