What is an osculating circle?

B

burt

Full Member
Joined
Aug 1, 2019
Messages
254
I'm learning calc III, and I don't understand what an osculating circle. I'm trying to read the book and understand it, but I simply am not! Can anyone explain it, or send me somewhere that will help me?
Thanks!
 
burt said:
I'm learning calc III, and I don't understand what an osculating circle. I'm trying to read the book and understand it, but I simply am not! Can anyone explain it, or send me somewhere that will help me?
Click to expand...
I think that you need to post an exact problem from the textbook you are following. It is unwise of us to guess at what you mean by the post.
 
pka said:
I think that you need to post an exact problem from the textbook you are following. It is unwise of us to guess at what you mean by the post.
Click to expand...
That's fair :)
I'm just trying to figure out what an osculating circle is. I don't have a specific problem - but I think I'm starting to understand a bit more. It's a circle that touches a point on a curve with the curvature of the curve at that point.
 
This is the problem I'm getting stuck on: Find the osculating circle at the given point: 1584677988014.png
This is my work so far: I know that I'm doing something wrong because I can't figure out any way to make a graph. The graph I made is definately wrong. Any direction?
Thanks!
1584677958645.png
 
burt said:
I'm learning calc III, and I don't understand what an osculating circle. I'm trying to read the book and understand it, but I simply am not! Can anyone explain it, or send me somewhere that will help me? Thanks!
Click to expand...
Have you looked at:

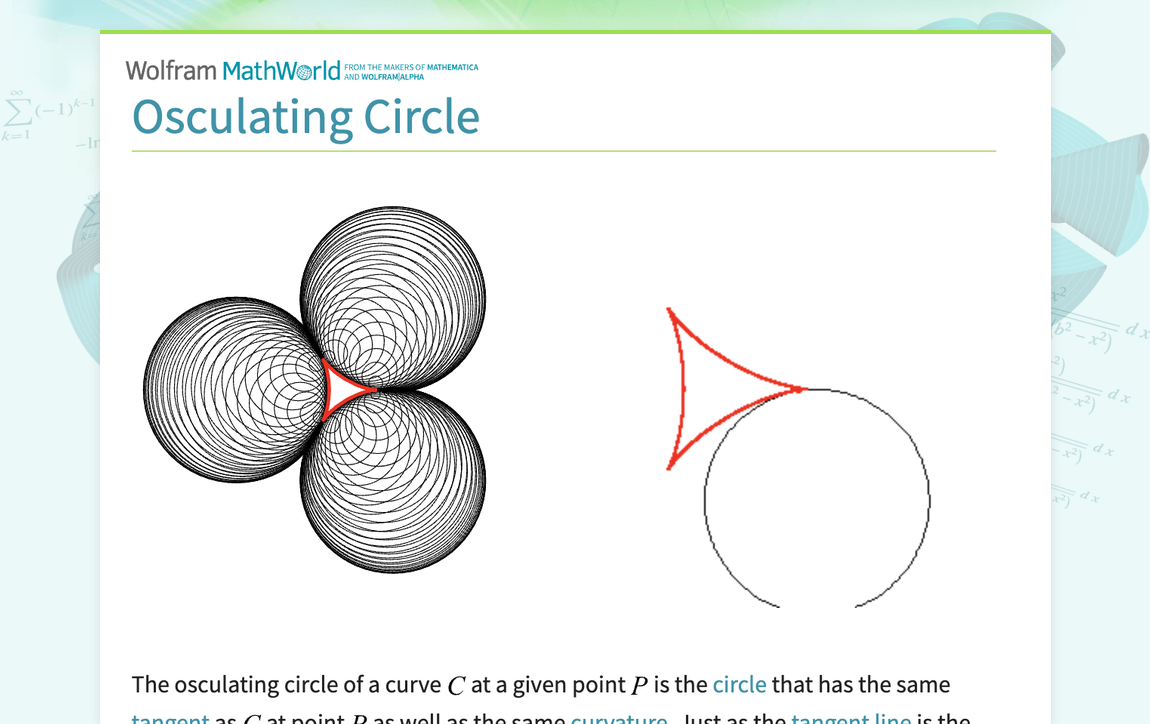
mathworld.wolfram.com

Osculating Circle -- from Wolfram MathWorld

The osculating circle of a curve C at a given point P is the circle that has the same tangent as C at point P as well as the same curvature. Just as the tangent line is the line best approximating a curve at a point P, the osculating circle is the best circle that approximates the curve at P...
mathworld.wolfram.com
 
Given a smooth curve, the tangent line at a given point on the line is a first degree curve that passes through the point and has the same direction, at that point, as the curve.

Given a smooth curve, the osculating circle at a given point on the line is a second degree curve that passes through the point, has the same direction, and has the same curvature, at that point, as the curve.

("Osculating" is from the Latin for "kissing". The curvature of a circle is 1 over the radius of the circle.)
 
HallsofIvy said:
Given a smooth curve, the tangent line at a given point on the line is a first degree curve that passes through the point and has the same direction, at that point, as the curve.

Given a smooth curve, the osculating circle at a given point on the line is a second degree curve that passes through the point, has the same direction, and has the same curvature, at that point, as the curve.

("Osculating" is from the Latin for "kissing". The curvature of a circle is 1 over the radius of the circle.)
Click to expand...
Thanks! Is it possible to show me an example? Because even with all this I'm still not understanding how to graph it - you can see in my earlier post that my graph is not quite an accurate one.
 
burt said:
Thanks! Is it possible to show me an example? Because even with all this I'm still not understanding how to graph it - you can see in my earlier post that my graph is not quite an accurate one.
Click to expand...
What is the form of a general of a 2nd degree function?
 
If y= f(x) then the curvature at \(\displaystyle (x_0, f(x_0))\) is \(\displaystyle \frac{\left(1+ \left(\frac{dy}{dx}\right)^2\right)^{3/2}}{\left|\frac{d^2y}{dx^2}\right|}\).

In the example you give, \(\displaystyle y= x^3\), \(\displaystyle \frac{dy}{dx}= 3x^2\), which equals 3 at x= 1, and \(\displaystyle \frac{d^2y}{dx^2}= 6x\), which equals 6 at x= 1, so the curvature of \(\displaystyle y= x^3\), at x= 1, is \(\displaystyle \frac{(1+ 3^2)^{3/2}}{6^2}=\frac{10^{3/2}}{36}\). So the radius of curvature, the radius of the osculating circle, is \(\displaystyle \frac{36}{10^{3/2}}\) or approximately 1.14.

We also need to calculate that the slope of the tangent line to \(\displaystyle y= x^3\) at (1, 1) is 3 so the tangent line is y= 3x- 2 and the perpendicular line is y= (4- x)/3. Measure a distance \(\displaystyle \frac{36}{10^{3/2}}\) along y= (4- x)/3 from (1, 1) to find the center of the osculating circle. How did you do that?
 
HallsofIvy said:
If y= f(x) then the curvature at \(\displaystyle (x_0, f(x_0))\) is \(\displaystyle \frac{\left(1+ \left(\frac{dy}{dx}\right)^2\right)^{3/2}}{\left|\frac{d^2y}{dx^2}\right|}\).

In the example you give, \(\displaystyle y= x^3\), \(\displaystyle \frac{dy}{dx}= 3x^2\), which equals 3 at x= 1, and \(\displaystyle \frac{d^2y}{dx^2}= 6x\), which equals 6 at x= 1, so the curvature of \(\displaystyle y= x^3\), at x= 1, is \(\displaystyle \frac{(1+ 3^2)^{3/2}}{6^2}=\frac{10^{3/2}}{36}\). So the radius of curvature, the radius of the osculating circle, is \(\displaystyle \frac{36}{10^{3/2}}\) or approximately 1.14.

We also need to calculate that the slope of the tangent line to \(\displaystyle y= x^3\) at (1, 1) is 3 so the tangent line is y= 3x- 2 and the perpendicular line is y= (4- x)/3. Measure a distance \(\displaystyle \frac{36}{10^{3/2}}\) along y= (4- x)/3 from (1, 1) to find the center of the osculating circle. How did you do that?
Click to expand...
Actually, as I work on this, finding the center is becoming a sticking point for me. Do I go that distance from the origin or from the point we are finding the circle at? If it is from the point, how do I find that center?
 
burt said:
Actually, as I work on this, finding the center is becoming a sticking point for me. Do I go that distance from the origin or from the point we are finding the circle at? If it is from the point, how do I find that center?
Click to expand...

As HallsofIvy pointed out, the center of the circle will lie along the line perpendicular to the tangent line, and which also passes through \((x_0,f(x_0))\). This is the normal line.

If \(r\) is the radius of the osculating circle, the point \((x_C,y_C)\) and \(y=mx+b\) is the normal line, then you will need to solve:

[MATH](x_C-x_0)^2+(mx_C+b-f(x_0))^2=r^2[/MATH]
and take the appropriate root to find the center of the circle.
 
HallsofIvy said:
If y= f(x) then the curvature at \(\displaystyle (x_0, f(x_0))\) is \(\displaystyle \frac{\left(1+ \left(\frac{dy}{dx}\right)^2\right)^{3/2}}{\left|\frac{d^2y}{dx^2}\right|}\).

In the example you give, \(\displaystyle y= x^3\), \(\displaystyle \frac{dy}{dx}= 3x^2\), which equals 3 at x= 1, and \(\displaystyle \frac{d^2y}{dx^2}= 6x\), which equals 6 at x= 1, so the curvature of \(\displaystyle y= x^3\), at x= 1, is \(\displaystyle \frac{(1+ 3^2)^{3/2}}{6^2}=\frac{10^{3/2}}{36}\). So the radius of curvature, the radius of the osculating circle, is \(\displaystyle \frac{36}{10^{3/2}}\) or approximately 1.14.

We also need to calculate that the slope of the tangent line to \(\displaystyle y= x^3\) at (1, 1) is 3 so the tangent line is y= 3x- 2 and the perpendicular line is y= (4- x)/3. Measure a distance \(\displaystyle \frac{36}{10^{3/2}}\) along y= (4- x)/3 from (1, 1) to find the center of the osculating circle. How did you do that?
Click to expand...
I reworked my problem, but I'm getting different numbers than you. And, I don't know how to find that center! If I had it in vector form, then I could multiply the radius times N and add that to my point. But, I'm not in vector form.
1584898351403.png
This is my work so far.
 
That "\(\displaystyle 6^2\)" in the denominator was an error. It should be just "6".
 
You must log in or register to reply here.
Top