what is an integral?

M

matt000r000

Junior Member
Joined
Mar 18, 2009
Messages
52
i just want to say this straight forward: i am NOT in calculus. this is just for my extreme mathematical appetite.

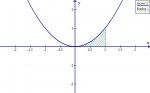
can some one explain what the integral does? i have wondered this for a year. what do the little-impossible-to-read numbers above and below the integral sighn mean? and i know integral has very much to do with finding the area of curves, but, specificly, how does it help you? i have looked at Principa, book 1: of the motion of bodies-section 1 (issac newton), and understand using the method of exaustion ad infinitum, but i don't see where integrals come in.i have also read lessons 3-4 and 21-24 Oeuvres completes d'augustin cuachy resume des lecons donnees a l'ecole royale polytechnique sur le calcul infinitesimal, where the integral is defined, but i still don't understand it. (both readings from Stephen Hawking's God Created the Integers: the mathematical breakthroughs that changed history)
 
It is an extremely vast topic. Google or grab any calc book and you can find lots.

But here is an easy example. Take the parabola y=x^2

Find the area from 0 to 1:

\(\displaystyle \int_{0}^{1}x^{2}dx=\frac{1}{3}x^{3}|_{0}^{1}=\frac{1}{3}(1)^{3}-\frac{1}{3}(0)^{3}=\frac{1}{3}\)

Here is the graph of the region we just found the area of. The 0 and 1 in the integral sign are the limits of integration.

If you are wondering how I got \(\displaystyle \frac{1}{3}x^{3}\) from \(\displaystyle x^{2}\), add 1 to the exponent and divide that into the coefficient.

It is directly related to the derivative. Take the derivative of \(\displaystyle \frac{1}{3}x^{3}\) and we are back to x^2.

To find the derivative, multiply the exponent by the coefficient and then subtract 1 from the exponent. See?. the opposite of integration. Get a calc book and start practicing and learning.

This is too vast a topic to explain here. As I said, google or find a good calc book. I would suggest something other than Newton's Principia for a beginner.

By the way, that is pronounced PRIN-KIP-E-UH, not PRIN-SIP-E-UH

Since you seem to love math, you will really like calc. That is when my interest in math piqued...when I took calc way back when

Another thing it is useful in is finding volume of some irregularly shaped object. That is called a volume or solid of revolution.

It is used in Physics all over the place. In economics. Just about everywhere math is involved. It's a beautiful thing. At least an egghead like me thinks so. I have always been amazed at the genius mind of Newton and his contemporaries that came up with it.
 

Attachments

  • para4.jpg
    para4.jpg
    19.5 KB · Views: 271
my mathematical mind burst as soon as the concept of the variable was itroduced. ever-since, i have been at least a grade-level above everyone else, and currently i am 2. im taking geometery and algebra 1 simultaniusly, for the most part understand the fundimentals of calculus, and am starting to learn algebra 2 on my own time. ironicly, this is how my math learning goes: i learn something myself or find it on my own, and then a while later the teacher acctually teaches it. if you give me any math text book, i will sometimes forget to eat or sleep sponging in the math. so, you might say i like math.... :D

thanx for the help!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

P.S.
-also ironicly, before i was introduced to the variable, i despised math with all the hatred i could muster! i still hate arithmatic and thank god for calculators!
 
I enjoy hearing you like it so. You will go far. Every journey begins with the first step. Eventually, you will get your doctorate in math.

Just think of all that waits. Differential equations, Complex Analysis, Abstract Algebra or Group Theory, Combinatorics and Probability, Linear and/or Matrix Algebra, on and on and on....................

Get on Amazon and try to find a Calculus book by James Stewart or Larson and Hostetler. A past edition should be inexpensive and they are two of the best published with good examples and all.
 
The best calculus book for a beginner i found - inspite of the name -

"Calculus for Dummies"
 
galactus said:
Just think of all that waits. Differential equations, Complex Analysis, Abstract Algebra or Group Theory, Combinatorics and Probability, Linear and/or Matrix Algebra, on and on and on....................
Click to expand...
i already know group theory. differential equations i kinda understand.

and i believe you- "____ for dummies" are the best explination books for almost any topic!
 
Its odd to me that you "understand" group theory before having taken the "standard" stream of math classes, and that you are in Algebra I. Is Algebra I "Modern/Advanced Algebra I" or are you referring to the standard "Algebra I."

Group theory is vast in itself. Did you mean you know what "Groups" are? That's very good, I hadn't heard of groups until 2 years AFTER Calculus. Keep going how you're going, and you'll do well. I will be a Grad student next semester, feel free to PM me.
 
i read a lot of math books. i understand what groups are and what most implications are from that. (i learned that from the language of mathmatics) i spent all of last night learning about differentials, and found a web site that has all of calculus on it. btw, i learn almost nothing from algebra I. i learn most everything from reading ahead in a textbook, searching the internet, reading a math book, watching 3 hours of discovery networks a day, and the only sacrafice i make is a social life. i am very content with my lot in life!

to prove it to you: (im a litle rusty. i read it a year ago)

a group is an instance that fills these conditions:
-for every member x, there must be a corrisponding -x (or opposite of x, as the case may be)
-there must exist a null member, such that, where n is the null member and x is any member, n+x=x
-its members must be accociative

an example of a group is transformations in geometry. for example:
-rotating 360[sup:zcsb4n8r]o[/sup:zcsb4n8r] is a null member. rotating 0 degrees is also a null member.
-the opposite of rotating 100 degrees is rotating -100, returning back to the begining(proving that, if members x and y are combined, they cancel out, thus proving they are inverses, aka: x+y=n, thus x=-y and y=-x, thus proving they are inverses).
-rotating is accociative, because rotating 50 degrees and then 100 degrees is the same as 100 degrees then 50 degrees.

also, integers are a group and real numbers are a group. so are all the other transformations, and transformations in general

i didn't think it was very important when i read it... it took me all of 5 seconds to understand. i thought it was essentially a mathematical template so the same rules and functions didn't have to be proven over and over again for similar things. it is used in mathematical topography, the study of the properties of a shape that stay contsant when undergoing any transformation or stretching, and is also used in the mathematical study of knots, both of which i have read about. i didn't realize the importance of what i was reading in that book! i might as well throw in that i know mathematical logic, and it too is a group.
 
I can see you enjoy math. That is good. Got another question?.

I would suggest, get a good book on calculus. Start at the beginning and go through it and do problems until you have each section down pat.

By the time you take the course, you can test out of it. :D That is what I done with calc I. I self-taught. I am certain you will ace it if you study and that should not be a problem.

Calc I deals with derivatives(differentiation, Newton's method, limits, etc); Calc II is where the integration comes in(Riemann sums, solids of revolution, area under a curve, etc.); Calc III is about vector calc, double and triple integrals, partial derivatives and so on.
 
You must log in or register to reply here.
Top