In the following:
(A scan of the original is attached.)
_______________________
Edited by stapel -- Reason for edit: Removing obscenity, copying text from image into post.
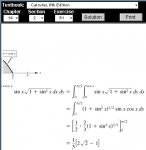
What happened to the "sin(x) cos(x)"?\(\displaystyle \sin{(x)}\, \sqrt{1\, +\, \sin^2{(x)}}\, dx\, dy\)
\(\displaystyle =\, \int_0^{\frac{\pi}{2}}\, \int_0^{\cos{(x)}}\, \sin{(x)}\, \sqrt{1\, +\, \sin^2{(x)}}\, dy\, dx\)
\(\displaystyle =\, \int_0^{\frac{\pi}{2}}\, \left(1\, +\, \sin^2{(x)})\right^{\frac{1}{2}}\, \sin{(x)}\, \cos{(x)}\, dx\)
\(\displaystyle =\, \left[\frac{1}{2}\, \dot\, \frac{2}{3}\, \left(1\, +\, \sin^2{(x)})\right)^{\frac{3}{2}}\right]_0^{\frac{\pi}{2}}\)
\(\displaystyle =\, \frac{1}{3}\, \left(2\sqrt{2}\, -\, 1\right)\)
(A scan of the original is attached.)
_______________________
Edited by stapel -- Reason for edit: Removing obscenity, copying text from image into post.