volume rotating about an axis! help!!!

[mculve1]

PLEEEAASSEEE help, cant figure this problem out at all.

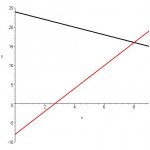
Find the volume of the solid obtained by rotating the region enclosed by the graphs of y=24-x, y=3x-8, x=0 about the y-axis.


I figured out where the two lines intersect at x=8 and tried to do the integral of (24-x)^2 - (3x-8)^2 from 0 to 8 but that was wrong.

 

[BigGlenntheHeavy]

\(\displaystyle Disc:\)

\(\displaystyle \pi\int_{16}^{24}(24-y)^2dy \ + \ \pi\int_{-8}^{16}\bigg(\frac{y+8}{3}\bigg)^2dy \ = \ \frac{2048\pi}{3}\)

\(\displaystyle Shell:\)

\(\displaystyle 2\pi\int_{0}^{8}x[(24-x)-(3x-8)]dx \ = \ \frac{2048\pi}{3}\)

\(\displaystyle See \ graph:\)

[attachment=0:2d6164e0]abc.jpg[/attachment:2d6164e0]