volume rotating about a line

[mculve1]

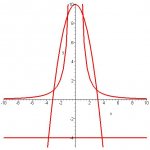
Fine the volume of the solid obtained by rotating the region enclosed by the graphs of y = 9/(x^2) and y = 10-x^2 about the line y= -4

I still am horrible at these problems.

Found the intersection is at x=1 and x=3 and tried to do the shell method, but i dont know how to account for the hole of the rotation down to y = -4

 

[BigGlenntheHeavy]

\(\displaystyle Washer:\)

\(\displaystyle 2\pi\int_{1}^{3}[(14-x^2)^2-(9/x^2+4)^2]dx \ = \ \frac{2752\pi}{15}\)

\(\displaystyle Shell:\)

\(\displaystyle 4\pi\int_{1}^{9}(y+4)\bigg[\sqrt{10-y}-\frac{3}{\sqrt y}\bigg]dy \ = \ \frac{2752\pi}{15}\)

\(\displaystyle See \ graph:\)

[attachment=0:1fy6lwom]def.jpg[/attachment:1fy6lwom]