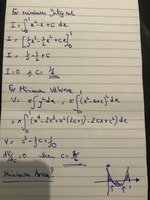volume of revolution problem

A

apple2357

Full Member
Joined
Mar 9, 2018
Messages
540
I am working on a problem..

Suppose y= x2 -x +c ( c is some constant).
I am interested in working out the value of c such that the volume of revolution when the curve above is rotated completely about the x axis between 0 and 1 is a minimum.
I have done the algebra and found the value of c is 1/6
Then i thought what value of c would give the integral between 0 and 1 to be a minimum and that turns out to be 1/6 too? Is this obvious?

Next, i am thinking about what value of c give the area enclosed between 0 & 1, exploring on software and this is not 1/6 but i can't see any easy way of how to do this problem and i don't understand why it is not the same?

Does this make any sense?
 
Does integral with c = 1/6 equal 0? Is this what you expected?
 
Can we see your work so we verify what you are saying is correct?
 
Jomo said:
You were asked two questions but only replied with one answer.
Click to expand...

Not sure, I did put the integral =0 and it made sense that a minimum integral might mean a minimum volume so yes but still don't quite no why.
 
apple2357 said:
Not sure, I did put the integral =0 and it made sense that a minimum integral might mean a minimum volume so yes but still don't quite no why.
Click to expand...
Again, you were asked two questions (please read the post) but only answered one.
Let's move past that. Can we please see your work? Note that this is the 2nd time I asked to see your work. Please, just show it to us.
 
My working was along these lines. I used the volume of revolution formulae and squared y, integrated to get
(1/5x^5-1/2x^4+x^3/3(2c+1)-cx^2+c^2x).
I put in the limits and got a quadratic c^2-1/3c+1/30 which has a minimum at c=1/6

The integral was the same thing but without squaring and that gave c=1/6 in a linear equation =0
 
Last edited:
Jomo said:
Again, you were asked two questions (please read the post) but only answered one.
Let's move past that. Can we please see your work? Note that this is the 2nd time I asked to see your work. Please, just show it to us.
Click to expand...

I think i am not surprised that a minimum integral gives a minimum volume but i think the minimum area should correspond to minimum volume? Sorry i know i am not being clear about it!
 
apple2357 said:
My working was along these lines. I used the volume of revolution formulae and squared y, integrated to get
(1/5x^5-1/2x^4+x^3/3(2c+1)-cx^2+c^2x).
I put in the limits and got a quadratic c^2-1/3c+1/30 which has a minimum at c=1/6

The integral was the same thing but without squaring and that gave c=1/6 in a linear equation =0
Click to expand...
Please post your actual work. It is not fair to me to do the work myself to verify your claims. Just post via an image your actual work. That will be very helpful and get you better responses.
 
apple2357 said:
I think i am not surprised that a minimum integral gives a minimum volume but i think the minimum area should correspond to minimum volume? Sorry i know i am not being clear about it!
Click to expand...
When c=1/6 you get 3 pieces: 2 above x axis (corresponds to positive area), 1 below (negative area). Their sum is 0. I would say you are finding 0 integral and volume, not minimum.
The software you are using might be disregarding signs, so there the area is always positive and the the minimum is somewhere other than 1/6.
 
I know i am finding zero integral as i set it equal to zero, but i am not sure why i am finding zero volume?
 
I wish that you had worked out that 2nd integral. In any case I did, you got the correct result and yes the min volume does occur at c=1/6.
However I do not agree that the are area integral is a min at c=1/6. After all, the less that c is results in the graph goes lower yielding a smaller area. That is you did not allow the area to go negative. This will happen in c<1/6
But having said that I find it suspicious that the area is zero precisely where the volume is min.
Try this out with a general quadratic and see if you get a similar result. That is let f(x) = ax^2 + bx + c, where a and b are constants and c can vary as a constant.
 
lev888 said:
When c=1/6 you get 3 pieces: 2 above x axis (corresponds to positive area), 1 below (negative area). Their sum is 0. I would say you are finding 0 integral and volume, not minimum.
The software you are using might be disregarding signs, so there the area is always positive and the the minimum is somewhere other than 1/6.
Click to expand...
I claim that there is no min since as c goes to neg infinity that area gets more and more negative.
 
You must log in or register to reply here.
Top