Volume of revolution of a solid

[SeekerOfDragons]

I'm having some trouble setting up and solving the following problem:

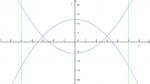
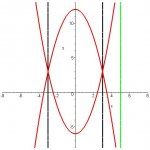
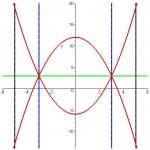
Find the volume of the solid formed by revolving the region between the curves y = 12 - X^2 and y = X^2 - 6 about the line X = 5 from [-5, 5]

There are 3 regions that will have an area between the two curves. will that mean I need to perform 3 calculations and add them together? such as calculate using the washer method the area from -5 to -3, then from -3 to 3, and finally from 3 to 5?

I'm just about totally lost on how to set up this problem since there are 3 different areas that will have a volume and rotating it about X=5 is throwing me off a bit too.

any advice on getting started and solving would be greatly appreciated.

 

[chrisr]

Isn't there just one area "between" the curves?
from -3 to 3.

 

[SeekerOfDragons]

yes, but the problem I'm trying to solve is including the little bit of area between them from [-5, -3] and [3, 5]

 

[chrisr]

The curves themselves have a single ovelap from x = -3 to 3, as one is upside- down relative to the other.
There is a part between the curves and the line x=5.
I don't think the question is expecting you to rotate that also, however.

I would expect you only need calculate the volume of the "doughnut".
From x=-3 to -infinity, one curve goes to infinity while the other goes to -infinity.

 

[SeekerOfDragons]

hmm. I'll double check with my instructor tomorrow evening and verify, but fairly sure all 3 regions are wanted. the full text as written in the problem is "Find the Volume of the solid formed by revolving the region shown in #5 about the line x=5"

Problem #5 it is referring to states "Find the area of the shaded region." with a picture showing the curves y = 12 - X^2 and y = X^2 - 6 both from -5 to 5. and in the picture all 3 regions are shaded.

 

[chrisr]

[attachment=0:2nvkz2g8]vor.jpg[/attachment:2nvkz2g8]The curves stop at x=-5 and x=5 ?
So you want to calculate the area between the curves and the lines x=-5 and x=5 also,
then rotate the 3 shaded areas around the line x=5.
Would that be it?

A convenient way to calculate area in situations like this is...

1. Integrate (x[sup:2nvkz2g8]2[/sup:2nvkz2g8]-6)-(12-x[sup:2nvkz2g8]2[/sup:2nvkz2g8]) from -5 to -3.
2. Integrate (12-x[sup:2nvkz2g8]2[/sup:2nvkz2g8])-(x[sup:2nvkz2g8]2[/sup:2nvkz2g8]-6) from -3 to 3.
3. Integrate (x[sup:2nvkz2g8]2[/sup:2nvkz2g8]-6)-(12-x[sup:2nvkz2g8]2[/sup:2nvkz2g8]) from 3 to 5.

As the graph is symmetrical about the y axis, you don't need to work out (3).

The sum of those integrals gives the 2-D area. Then you can rotate that.

The reason you subtract is to sum the "difference" between them between the points of intersection,
giving you the shaded region areas.

 

[SeekerOfDragons]

Chrisr,

That is the correct picture of the problem that I'm trying to rotate. I've already managed to calculate the area of the 3 regions to be 392/3 Units^2

My issue arises in that I don't know how to do the rotation.

 

[chrisr]

When you are rotating this shape about the axis x=5,
you don't need to know those 3 areas.
All the points in the shape trace out circles about the axle x=5.
You need the radii of the circles to get the cross-sectional areas of the discs and rings.
You need to study how the cross-sectional areas look,
then calculate radii, from the line x=5, work out cross-sectional areas,
finally integrating all of those discs (for the part against x=5)
and rings (for the other 2 areas) from y=5[sup:29qpcatl]2[/sup:29qpcatl]-6 to y=12-5[sup:29qpcatl]2[/sup:29qpcatl].

 

[chrisr]

When continuing, you need to realise that the graph is not symmetrical about the line y=3,
this is because the curves don't intersect midway between the upper and lower vertical bounds
of the shape as it rests against x=5.

Correction!! it is symmetrical, the curves are the same ones upside down, sliding up and down the vertical axis.

You can rotate each "part of the shape" independently.

You could also move the shape against the y-axis, standing on the x-axis if you like.

As an example, take the region bounded within the points (3,3), (5,3) and (5,19).
This is the top part of the rightmost "handle".

You must derive a formula for the radius of each disc from y=3 to y=19 formed by the rotation,
where the centre of the disc is (5,y).

Since y=x[sup:nqjcl835]2[/sup:nqjcl835]-6,
x[sup:nqjcl835]2[/sup:nqjcl835]=y+6,
x=sqrt(y+6) and the radius of the disc is 5-sqrt(y+6).
The disc cross-sectional area is (pi)r[sup:nqjcl835]2[/sup:nqjcl835]=(pi){5-sqrt(y+6)}[sup:nqjcl835]2[/sup:nqjcl835].
The volume of revolution of that part is the integral of those discs from y=3 to y=19.

Continue for the lower part, just double your answer.
Then you need to calculate "differences" of disc areas for the outer pair of rings.
It's the same procedure for calculating radius.

 

[SeekerOfDragons]

ok,

I'm not close to sure if I've got the first part of it right, but for the area between x=3 and x=5, rotated around x=5 I got 1344pi

Got that by:
pi * Integral (3, 19) (5 - sqrt(y + 6))^2 dy

factoring that out and simplifying (assuming i did it correctly) i got:
pi * Integral (3, 19) (y - 10 * sqrt(Y + 6) + 31) dy

converts to:

(y^2)/2 - 20(y + 6)^(3/2)/3 + 31y ] (3, 19) * pi

this evaluates out to 56pi/3

Next I evaluated:
pi * Integral (-13, 3) (5 - sqrt(12 - y))^2 dy

factoring that out and simplifying (assuming I did it correctly) i got:
pi * Integral (-13, 3) (-y - 10 * sqrt(12 - y) + 37

converts to:

(-y^2)/2 - 20(12 - y)^(3/2)/3 + 37y ] (-13, 3)

this evaluates out to 3976pi/3

to find whole area of the first half:
56pi/3 + 3976pi/3 = 1344pi

am I even close to getting that correct?

 

[BigGlenntheHeavy]

\(\displaystyle Upper \ half \ (y \ \ge3), \ then \ double \ it \ as \ the \ bottom \ half \ is \ just \ a \ reflection \ of \ the \ top \ half\)

\(\displaystyle Disc:\)

\(\displaystyle \pi\int_{3}^{19}[\sqrt(y+6)-5]^{2}dy \ = \ \frac{56\pi}{3}.\)

\(\displaystyle Washer:\)

\(\displaystyle \pi\int_{3}^{12}[(0-5)^{2}-(\sqrt(12-y)-5)^{2}]dy \ = \ \frac{279\pi}{2}\)

\(\displaystyle Washer:\)

\(\displaystyle \pi\int_{3}^{12}[(-\sqrt(12-y)-5)^{2}-(0-5)^{2}]dy \ = \ \frac{441\pi}{2}\)

\(\displaystyle Washer:\)

\(\displaystyle \pi\int_{3}^{19}[(-5-5)^{2}-(-\sqrt(y+6)-5)^{2}]dy \ = \ \frac{824\pi}{3}\)

\(\displaystyle Shell Method:\)

\(\displaystyle Shells:\)

\(\displaystyle 2\pi\int_{3}^{5}[(x^{2}-9)(5-x)]dx \ = \ \frac{56\pi}{3}\)

\(\displaystyle Shells:\)

\(\displaystyle 2\pi\int_{0}^{3}[(9-x^{2})(5-x)]dx \ = \ \frac{279\pi}{2}, \ Note: \ 2nd \ and \ 3rd \ shells \ can \ be \ done \ as \ one.\)

\(\displaystyle Shells:\)

\(\displaystyle 2\pi\int_{-3}^{0}[(9-x^{2})(5-x)]dx \ = \ \frac{441\pi}{2}\)

\(\displaystyle Shells:\)

\(\displaystyle 2\pi\int_{-5}^{-3}[(x^{2}-9)(5-x)]dx \ = \ \frac{824\pi}{3}\)

\(\displaystyle Ergo, \ Volume \ = \ 2\bigg(\frac{56\pi}{3}+\frac{279\pi}{2}+\frac{441\pi}{2}+\frac{824\pi}{3}\bigg) \ = \ \frac{3920\pi}{3}.\)

\(\displaystyle Seeker \ of \ Dragons, \ if \ these \ are \ the \ problems \ your \ Professor \ gives \ you, \ he \ must \ indeed \ be\)

\(\displaystyle a \ harsh \ taskmaster.\)

\(\displaystyle See \ graph. \ Note: \ Second \ graph \ is \ best.\)

[attachment=1:3qvrsxny]yza.jpg[/attachment:3qvrsxny]

 

[SeekerOfDragons]

Definitely a difficult professor. I'm usually a pretty decent math student, but combining taking calc as a night class (2.5 hours twice a week after a full day of work) and a professor that goes a bit fast and tosses out fairly difficult problems... tons of fun.

I greatly appreciate your help with this question and verifying my answers over the last week or two.

I did have a question about the integrals you provided. you provided 4 separate integrals. am I correct in assuming that there is one for the area between [x= -5 and x= -3], [x=-3, and x=0], [x=0, x=3], and [x=3, x=5]?

 

[chrisr]

Performing the integration by hand, I got 18.7(pi) for the part between (3,3), (5,3) and (5,19),
I don't have an integrating device.

The graph is in fact symmertical about y=3, so the volume of revolution of the part flush against x=5 is
37.4(pi) by my hand calculations.
Then you move onto the two rings.

Glenn has answered (I was typing this up at the time).
His answers should be spot on.

In answer to your last question, from -5 to -3 on the x-axis,
though that shape is the same as the one against the line x=5,
it will trace out a "ring" shape as opposed to a disc.
The radii are far greater when you rotate "that part" around x=5.

 

[BigGlenntheHeavy]

Hey, Seeker of Dragons, there might be an easier way, but I don't know it. I did the four regions by the washer-disc method and then by the shell method, as a check. Either method can be used, use your own discretion.

Note: Did some editing above, answers should be correct now.

\(\displaystyle Note: \ Figured \ out \ the \ easiest \ way, \ I \ think.\)

\(\displaystyle All \ Shells, \ to \ wit:\)

\(\displaystyle 2\pi\int_{-5}^{-3}[(x^{2}-6)-(12-x^{2})](5-x)dx \ = \ \frac{1648\pi}{3}\)

\(\displaystyle 2\pi\int_{-3}^{3}[(12-x^{2})-(x^{2}-6)](5-x)dx \ = \ 720\pi\)

\(\displaystyle 2\pi\int_{3}^{5}[(x^{2}-6)-(12-x^{2})](5-x)dx \ = \ \frac{112\pi}{3}\)

\(\displaystyle Hence, \ Total \ Volume \ = \ \frac{1648\pi}{3}+720\pi+\frac{112\pi}{3} \ = \ \frac{3920\pi}{3}\)

 

[SeekerOfDragons]

Big Glenn,

I have a couple questions regarding the answers you provided. I'm attempting to use the disk and washer methods to start with.

for the first region from x=3 to x=5, why is it (sqrt(y + 6) - 5) instead of (5 - sqrt(y + 6)? Either way, I came up with the same answer, but wasn't sure if it was just a fluke in this case or true all the time?

then for the second region from x=0 to x=3, i'm not sure how you calculated the order of the two radii

I may be a bit confused, but my understanding was to take the outer radius and subtract the inner radius.

I would think the outer radius would be (5 - sqrt(12 - y)) and the inner would be (0 - 3)?

am I looking at the picture wrong or just misunderstanding the whole washer method?

 

[SeekerOfDragons]

hmmm. wait a bit... I'm still wondering about the "why is it (sqrt(y + 6) - 5) instead of (5 - sqrt(y + 6)" part of my original question, but looking at the picture and analyzing it, it may have clicked as to why you had it in the order you had it...

the outside of the ring in relation to x=5 would be the y-axis. as such the big radius would be (0 - 5). The little radius would be wherever the function y = 12 - X^2 is at that instant. of course it had to be put into x = sqrt(12 - y) and putting it in relation to x=5 the little radius would then be (5 - sqrt(12 - y))

am i looking/understanding it correctly?

 

[BigGlenntheHeavy]

SeekerofDragons, Use my thread where I prove what the volume of the equation was by using the method of shells, I used three, to solve the problem and I think it was the easiest and fastest way to go. It is a couple of threads back, and oh, by the way (x-y)^2 = (y-x)^2.

 

[SeekerOfDragons]

big glen,

ah. knew that. just needed a memory jogger I guess.

just for my information though, if I was just wanting the radius not the radius^2, which version would be correct?

I'll try to use the shell method here on that problem shortly once I learn how it works ( missed that day of lecture due to work ) In the mean time, i'll use the integrals you provided for the washer/disk method since I've actually worked them all out and wonder of wonders came up with the answer you provided. just a matter of figuring out why in regions 3 and 4 the sqrt(whatever) part turns out negative. I'm surmising it's because it's to the left of the y-axis, but i could be wrong.

 

[BigGlenntheHeavy]

\(\displaystyle Look, \ equation \ of \ a \ circle: \ x^{2}+y^{2} \ = \ 1\)

\(\displaystyle Hence, \ above \ the \ x-axis \ we \ have \ y \ = \ \sqrt(1-x^{2}) \ and \ below \ the \ x-axis \ we \ have \ y \ = \ -\sqrt(1-x^{2}).\)

\(\displaystyle Now, if \ x \ = \ y^{2}, \ then \ y \ = \ x^{1/2} \ above \ the \ x-axis \ and \ y \ = \ -x^{1/2} \ below \ the \ x-axis.\)

 

[chrisr]

Hi Seekerofdragons,

you are probably clear on this piece already,
but in calculating the radius for the discs resulting from rotating the rightmost part
of your shape (which touches the line x=5), x is <5, so r=5-x, which is 5-sqrt(y+6),
but as Glenn pointed out, z[sup:17wxikt6]2[/sup:17wxikt6]=(-z)[sup:17wxikt6]2[/sup:17wxikt6], so it does not matter how you set up the subtraction
if you are going to square the result, but the radii of the discs are 5-sqrt(y+6).
They are also 5-sqrt(12-y).

Notice how Glenn calculated the volume of revolution of the centre shape, using the "washer" method.
He rotated the part against the y-axis and extending to x=3 seperately from the part
against the y-axis extending to x=-3.
He can then sum the volumes, having rotated these.

As he mentioned, there are alternative ways to do this.

What I was thinking was to get the radius of the leftmost side of that shape (to the left of the y-axis), which is 5+x,
for x positive,
it's distance from the line x=5,
calculate the area of the disc of that radius,
then calculate the radius from x=5 to the right edge of the centre piece, which is 5-x, for x positive,
calculate the area of that disc,
then subtract the area of the smaller disc from the larger one to get the surface area of the washer.


Does that help in any way?

Then integrate those washers over the appropriate range of y.