volume of a solid

[raspberries]

hi, i have this question that i'd really appreciate if someone could help me with. here it is:
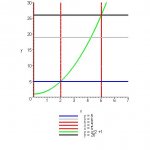
find the volume of the solid of revolution if the region bounded by y=x^2+1, y=5. y=26, and x=0 is rotated about the y-axis. then, find K to the nearest thousandth where the line y=K would be rotated to cut this solid into one-half its volume.

so when i did volume by disks, i got 304.5pi units cubed... is that right? and for finding y=K, i have no idea! do i work with the same integral?

 

[BigGlenntheHeavy]

$\displaystyle Shells:$

$\displaystyle V \ = \ 2\pi\int_{0}^{2} x(26-5)dx+2\pi\int_{2}^{5} x[26-(x^{2}+1)]dx \ = \ \frac{609\pi}{2}.$

$\displaystyle Discs:$

$\displaystyle V \ = \ \pi\int_{5}^{26}(\sqrt{y-1})^{2}dy \ = \ \frac{609\pi}{2}$

$\displaystyle \frac{V}{2} \ = \ \frac{609\pi}{4}$

$\displaystyle \frac{609\pi}{4} \ = \ \pi\int_{k}^{26}(\sqrt{y-1})^{2}dy, \ k \ = \ 18.9025$

$\displaystyle Check: \ \frac{609\pi}{4} \ = \ \pi\int_{5}^{k}(\sqrt{y-1})^{2}dy, \ k \ = \ 18.9025$

$\displaystyle See \ graph$

[attachment=0:slcyi96p]abc.jpg[/attachment:slcyi96p]

 

[mmm4444bot]

so when i did volume by disks, i got 304.5pi units cubed ... is that right? Looks good.

I would report the volume as 956.6 cubic units, but that's me.



and for finding y=K, i have no idea! do i work with the same integral? Yes, only you're integrating from y = 5 to K.

That has to equal half the known volume. Solve for K.

 

[raspberries]

thank you both!!