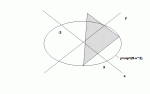
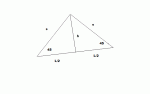
Find the volume of the solid whose base is bounded by the circle x^2+y^2=9 and cross section areas are isosceles right triangles perpendicular to the x-axis?
I am having trouble picturing this figure, i am usually good with geometry type things but i just cannot picture this.
It would be great if someone could help me out with what solid i need to find the volume of and maybe which method to use (shell, washer, etc.)
I am having trouble picturing this figure, i am usually good with geometry type things but i just cannot picture this.
It would be great if someone could help me out with what solid i need to find the volume of and maybe which method to use (shell, washer, etc.)