Volume of a solid and fluid pressure

L

lamaclass

Junior Member
Joined
Oct 18, 2009
Messages
69
I'm unsure of how to go about setting up these two problems:

1. Two identical cones with a height of 2 and a base circle of a radius of 2 are glued together at their bases and a cylindrical section of radius 1 is cut out along the axis of the resulting object. Set up and evaluate an integral(s) to determine the volume as a solid of revolution.

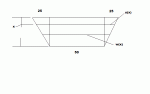
2. A dam is inclined at an angle of 30 degrees from the vertical and has the shape of an isoceles trapezoid 100 ft wide at the top and 50 ft wide at the bottom. It also contains a slant height of 70 ft. Find the fluid force on the dam when it is full of water. Weight density of water is 62.4 lbs/ft[sup:2h3eaw8w]3[/sup:2h3eaw8w].
 
1. Two identical cones with a height of 2 and a base circle of a radius of 2 are glued together at their bases and a cylindrical section of radius 1 is cut out along the axis of the resulting object. Set up and evaluate an integral(s) to determine the volume as a solid of revolution.
Click to expand...

Draw a sketch of this object’s cross-section on an xy-graph, centered on the origin.

In the first quadrant, you will find a triangle of the cross-section. Rotate this shape around the y-axis, then double your answer to account for the bottom half of the object.
 
Thanks wjm11! So would I want to apply the Shell method in this case since we're parellel to the y-axis?
 
So would I want to apply the Shell method in this case since we're parellel to the y-axis?
Click to expand...

The shell method should work fine.

You could also write your equations in terms of x if you wanted to, and integrate with respect to y -- using the washer method. Your choice.
 
For #2, w(x)=50+2u(x).

Use similar triangles to find u(x) in terms of x. Remember, take the incline of 30 degrees into account.

Then, you can sub u(x) into the expression for w(x) and set up the integral.

Here is a diagram.
 

Attachments

  • dam.gif
    dam.gif
    3.3 KB · Views: 274
Thanks for your help too Galactus!

On the first one I got confused on the functions when applying the washer method. :?

ETA: Never mind I see you could use slope!
 
lamaclass said:
For the first one, I got an answer of 64 pi/3. Is that correct? Nope.
Click to expand...

The combined volume of two cones with radius 2 and height 2 is only 16 Pi/3 cubic units. And that's before drilling out the cylindrical hollow through their center.

At the very least, your result is 4 times too big.

Did you remember to subtract the "hole" ?

Please double-check your work, and if you find yourself stuck, I suggest that you show us what you did.

As far as choosing shells versus washers, you can orient the object any way you like. For example, when you think about drawing the y-axis going through the center of this object, but prefer washers, simply draw the x-axis going through the center, instead.

As a verification, we can also answer the first exercise (using the volume formulas for a cone and cylinder) by simply subtracting the two parts that get drilled away from each cone.

Cylinder: V = Pi r^2 h

Cone: V = 1/3 Pi r^2 h

If I'm thinking correctly, according to my unproportional diagram below, half the volume you're looking for is that of the undrilled cone (8/3 Pi cubic units) minus the cylindrical hole (1/3 Pi cubic units) minus the upper part of the cone (Pi cubic units).

So, you can use the solution from that method as a check against your calculus result, yes?

(Double-click image, to expand)

[attachment=0:uqwb7dxs]Cone.JPG[/attachment:uqwb7dxs]
 

Attachments

  • Cone.JPG
    Cone.JPG
    22.3 KB · Views: 256
Would I need a total of 4 definite integrals to solve this problem? I'm still stuck. :(

Here's the work that I've done so far:

I drew out a diagram of where the two cones touch and then drew a representive rectangle showing where they all meet and the points I found were:
(-2, 0), (0,-2) (2,0) and (0,2)

Looking at the points (0,2) and (2,0), I applied the slope formula and slope-intercept formulas:

m = -1

y-y[sub:nn3pwz2q]1[/sub:nn3pwz2q] = m (x - x[sup:nn3pwz2q]1[/sup:nn3pwz2q])

= -1x+2

= 2pi IN limits 0 and 2, (-x+2)[sup:nn3pwz2q]2[/sup:nn3pwz2q]-4 dx

= x[sup:nn3pwz2q]3[/sup:nn3pwz2q]/3 +4x

=8/3+8 = 32/3 * 2pi = 64pi/3. Am I going about this problem in the wrong way?
 
\(\displaystyle 1) \ I \ am \ going \ with \ mmm4444bot's \ diagram, \ the \ volume \ of \ a \ hollow \ frustum \ by \ 2.\)

\(\displaystyle Shells:\)

\(\displaystyle V \ = \ 4\pi\int_{1}^{2}y(2-y)dy \ = \ \frac{8\pi}{3} \ cubic \ units\)

\(\displaystyle Discs:\)

\(\displaystyle V \ = \ 2\pi\int_{0}^{1}[(-x+2)^{2}-(1)^{2}]dx \ = \ \frac{8\pi}{3} \ cubic \ units\)
 
lamaclass said:
= 2 pi INT[limits 0 and 2, (-x+2)[sup:2t5kk2g3]2[/sup:2t5kk2g3] - 4 dx]
Click to expand...

We integrate only from 0 to 1 because there is no solid beyond 1 (the top part of the cone gets drilled away -- see my diagram).

Why are you subtracting 4 for the hole? The radius of the drill bit is only 1 unit.

Otherwise, your set-up looks good.
 
\(\displaystyle By \ the \ way \ mmm4444bot, \ good \ show \ with \ your \ diagram, \ as \ I \ had \ "a \ mental \ block" \ in \ trying\)

\(\displaystyle \ to \ figure \ out \ this \ one.\)
 
Ahh I see it now, thank you both very much! So 8pi/3 would be the final answer for 1 then right?
 
lamaclass said:
So 8pi/3 would be the final answer for 1 then right?
Click to expand...

Well, I'm not sure why you're still asking for confirmation.

Glenn already showed the answer, explicitly, using calculus.

I already showed the answer, implicity, using 2(8Pi/3 - Pi/3 - Pi).

Yes, your result is correct. 8-)
 
You must log in or register to reply here.
Top