Volume of a solid and arc length

[lamaclass]

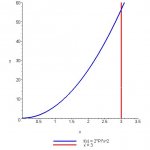
I am not sure how to do these two problems:

1. The volume of a solid is obtained by revolving a region in the first quadrant of the xy-plane about the x-axis. The resulting integral is IN, limits 0 and 3, 2 pi x[sup:4hrw3q8b]2[/sup:4hrw3q8b] dx. Graph the region being rotated.

2. The graph of y = f(x) passes through the origin. The arc length from (0,0) to (x, f(x)) is s(x) = IN, limits 0 and x, = sq. rt. of 1+e[sup:4hrw3q8b]t[/sup:4hrw3q8b]dt. Determine the function f(x).

 

[soroban]

Hello, lamaclass!

2. The graph of \(\displaystyle y = f(t)\) passes through the origin.

\(\displaystyle \text{The arc length from }t=0\text{ to } t=x\text{ is: }\; s(t) \:=\: \int^x_0 \sqrt{1\,+\,e^t}\,dt\)

\(\displaystyle \text{Determine the function, }f(t).\)

\(\displaystyle \text{Formula: }\;\;L(t) \;=\;\int^b_a\sqrt{1\,+\,\left[f'(t)\right]^2}\,dt\)


\(\displaystyle \text{So we have: }\;\left[f'(t)\right]^2 \;=\;e^t \quad\Rightarrow\quad f'(t) \:=\:e^{\frac{1}{2}t}\)

. . \(\displaystyle \text{Then: }\;f(t) \;=\;2e^{\frac{1}{2}t}+ C\)


\(\displaystyle \text{"Through the origin" means:}\:f(0)\,=\,0\)

. . \(\displaystyle \text{So we have: }\:2e^0\,+\,C \:=\:0 \quad\Rightarrow\quad C \:=\:-2\)


\(\displaystyle \text{Therefore: }\;f(t) \;=\;2e^\frac{1}{2}t} - 2\)

 

[lamaclass]

Thanks for your help Soroban!

 

[BigGlenntheHeavy]

\(\displaystyle 1) \ V \ = \ \ \pi \int_{0}^{3}[2\pi x^{2}]^{2}dx \ = \ \pi \int_{0}^{3}4 \pi^{2} x^{4}dx \ = \ 4\pi^{3}\int_{0}^{3} x^{4}dx\)

\(\displaystyle = \ \frac{4\pi^{3}x^{5}}{5}\bigg]_{0}^{3} \ = \ \frac{972\pi^{3}}{5}, \ See \ graph \ below.\)

[attachment=0:69xav0w8]vwx.jpg[/attachment:69xav0w8]

 

[lamaclass]

Thanks Glenn!