When we intersect two cylinders of the same radius, the cross sections are squares.
With axes through the center of one of the cylinders and perp. to the axis of the cylinder, with y
directed upwards, the squares have side length at level y of \(\displaystyle 2\sqrt{r^{2}-y^{2}}\).
The area of the cross section(area of square) of the intersection at level y is then:
\(\displaystyle A(y)=(2\sqrt{r^{2}-y^{2}})^{2}=4(r^{2}-y^{2})\)
This is what is to be integrated: \(\displaystyle 4\int_{-r}^{r}(r^{2}-y^{2})dy\)
Now, what is the volume of the cube the satellite is in?. Find it, then subtract the two volumes.
What remains is the unused portion.
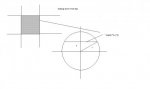
Here is a diagram to help picture what I am trying to describe.
The gray square is a cross section looking down from the top. The circle is looking in through a cylinder. The chord through the circle is a side of a square that makes a cross section.