Venn Diagram

[karlo]

[attachment=0:3dojodvj]venn1.GIF[/attachment:3dojodvj]

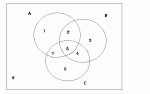
Given the elements of the set, find the operation involved.
1. {4,8} = B [intersection] C
2. {3,4} = B-A
3. {3,4,5} = (BUC)-A
4. {1} = A - (B U C)
5. {6} = (A U B U C)'
6. {1,5,6,7} = B'
7. {7} = (A [intersection] C)-(B [intersection] C)
8. {6,5} = (A U B)'
9. {1,3,6} = {[A [intersection] B] U C }'
10. {6,7,8} = [(A U B U C)- A (intersection) C]'
11. {1,2,3} =(A U B) - C
12. {2,8} = A (intersection) B
13. {1,6} = (B U C)'
14. {2,4,8} = A (intersection) B (intersection) C
15. {7,5} = C - (B (intersection) C
16. {6,8} = ???
17. {6,7} = ???
18. {4,5} = C - ( A (intersection) C)
19. {1,7,5} = A U C - B

PLEASE HELP. Kindly check my answers and tell if they are correct and if something is wrong pls. help me correct it.

 

[soroban]

Hello, karlo!

Given the elements of the set, find the operation involved.

\(\displaystyle 1.\;\{4,8\} \:=\: B \cap C\)

\(\displaystyle 2.\;\{3,4\} \:=\: B-A\)

\(\displaystyle 3.\;\{3,4,5\} \:=\: (B\cup C)-A\)

\(\displaystyle 4.\;\{1\} \:=\: A - (B \cup C)\)

\(\displaystyle 5.\;\{6\} \:=\: (A \cup B \cup C)'\)

\(\displaystyle 6.\; \{1,5,6,7\} \:=\: B'\)

These are all correct!

\(\displaystyle 7.\;\{7\} \:=\: (A \cap C) -(B \cap C)\)

This could be written: .\(\displaystyle A \cap C \cap B'\,\text{ or }\,(A\cap C) - B\)

\(\displaystyle 8.\;\{6,5\} \:=\: (A \cup B)'\)

\(\displaystyle 9.\;\{1,3,6\} \:=\: [A \cap B) \cup C]'\)

\(\displaystyle 10.\; \{6,7,8\} \:=\: [(A \cup B \cup C) - (A \cap C)]'\)

\(\displaystyle 11.\;\{1,2,3} \:=\A U B) - C\)

\(\displaystyle 12.\;\{2,8\} \:=\: A \cap B\)

\(\displaystyle 13.\;\{1,6\} \:=\: (B \cup C)'\)

These are all correct!

\(\displaystyle 14.\;\{2,4,8\} \:=\: A \cap B \cap C\) . . . . no

\(\displaystyle \{2,4,8\} \:=\A \cup C) \cap B\)

\(\displaystyle 15.\;\{5,7\} \:=\: C - (B \cap C)\)

This could be written: .\(\displaystyle C - B\)

\(\displaystyle 16.\;\{6,8\}\)

\(\displaystyle \{6,8\} \:=\A' \cap B' \cap C') \cup (A \cap B \cap C)\)

\(\displaystyle 17.\;\{6,7\}\)

This is just the union of the two "pieces".

\(\displaystyle \{6.7\} \;=\;(A' \cap B' \cap C') \cup (A \cap B' \cap C)\)

\(\displaystyle 18.\;\{4,5\} \:=\: C - ( A \cap C)\)

This can be written: .\(\displaystyle C - A\)

\(\displaystyle 19.\;\{1,5,7\} \:=\: (A \cup C) - B\) . Correct!

 

[karlo]

thank you so much!you are such a big help.