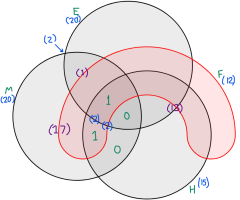
Could someone post how to solve a venn diagram?
The students studied
20 English
20 Math
15 History
12 French
2 Math and english
2 Math and history
2 Math, history and french
1 Math, English, history and french
How many students studied at least one subject
The students studied
20 English
20 Math
15 History
12 French
2 Math and english
2 Math and history
2 Math, history and french
1 Math, English, history and french
How many students studied at least one subject