Venn Diagram -phone in requests/hard rock/top 100

[Guest]

Jeffery works as a DJ at a local readio station. On occasion, he chooses some of the song recieved by the switchboard the previous day. Jeffery's list of 200 possible selections includes,

- all the songs in the top 100
-134 hard rock songs
-50 phone in requests
-45 hard rock songs in the top 100
- 20 phone in requests in the top 100
-24 phone in requests for hard rock songs

How many phone in requests were for hard rock songs in the top 100?

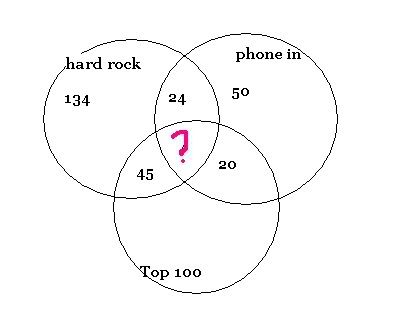
How do you do this question? Ill show you my venn diagram, but I need the middle number to figure out the rest of the numbers. So My venn diagram is not correct yet. But how do you figure out the middle number?

 

[pka]

If we use the letters T, H, P for “top 100”, “hard rock” & “phone in”, the we know the number is each. \(\displaystyle \left| T \right| = 100\), \(\displaystyle \left| H \right| = 134\), \(\displaystyle \left| P \right| = 50\), then \(\displaystyle \left| {T \cap H} \right| = 45\), \(\displaystyle \left| {T \cap P} \right| = 20\), \(\displaystyle \left| {P \cap H} \right| = 24\).

Now use the inclusion/exclusion rule:
\(\displaystyle \left| {T \cup H \cup P} \right| = \left| T \right| + \left| H \right| + \left| P \right| - \left| {T \cap H} \right| - \left| {T \cap P} \right| - \left| {P \cap H} \right| + \left| {T \cap H \cap P} \right|.\)

You know that \(\displaystyle \left| {T \cup H \cup P} \right| = 200\) so find \(\displaystyle \left| {T \cap H \cap P} \right|\)