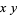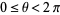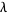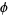Using Spherical Coordinates to Evaluate Triple Integral

[burt]

I was given the following problem:
Set up and evaluate the indicated triple integral in an appropriate coordinate system: \(\iiint_{Q}{\sqrt{x^2+y^2+z^2}dV}\) where \(Q\) is bounded by the hemisphere \(z=-\sqrt{9-x^2-y^2}\) and the \(xy\)-plane.

Here is the graph I made of \(Q\)

I'm struggling to figure out the limits of integration. It seems to me that \(\rho\) goes from \(0\) to 3 because the radius of the sphere is 3. It also seems to me that \(\phi\) extends from \(-\pi\) to \(0\). That is the one I'm most uncertain about - because it is the new element in spherical coordinates. \(\theta\) seems to be from \(0\) to \(2\pi\).
This makes my integral \(\int^{2\pi}_{0}\int^0_{-\pi}\int^3_0\rho^3\sin(\phi)\ d\rho\ d\phi\ d\theta\)

Are these limits correct?

 

[Dr.Peterson]

On your graph, pick a point on the sphere and mark the line segment formed as [MATH]\rho[/MATH] varies from 0 to 3. This will be a radius of the sphere.

Now mark what you get if you take this segment and let [MATH]\phi[/MATH] vary from -\pi to 0. It may not be what you expect, and you may choose to change that; or you may be happy with that.

Now think about what happens when you let [MATH]\theta[/MATH] vary from 0 to [MATH]2\pi[/MATH]. Will you exactly cover the hemisphere, once, or something else.

All of this is good experience! The mistake you've made is easy to make, and seeing it visually can help you avoid it in the future.

By the way, there are a few different ways to define spherical coordinates; I'm assuming I know how you define [MATH]\phi[/MATH], but you'll have to tell me what it is if we discuss this further.

 

[burt]

On your graph, pick a point on the sphere and mark the line segment formed as [MATH]\rho[/MATH] varies from 0 to 3. This will be a radius of the sphere.

Now mark what you get if you take this segment and let [MATH]\phi[/MATH] vary from -\pi to 0. It may not be what you expect, and you may choose to change that; or you may be happy with that.

Now think about what happens when you let [MATH]\theta[/MATH] vary from 0 to [MATH]2\pi[/MATH]. Will you exactly cover the hemisphere, once, or something else.

All of this is good experience! The mistake you've made is easy to make, and seeing it visually can help you avoid it in the future.

By the way, there are a few different ways to define spherical coordinates; I'm assuming I know how you define [MATH]\phi[/MATH], but you'll have to tell me what it is if we discuss this further.

I thought that \(\phi\) is the angle up and down, and \(\theta\) is the angle side to side. But, based on what you are saying it seems that I a wrong. I looked at the link you attached (thank you!) and I've been trying to figure it all out - but can you help me out?

 

[Dr.Peterson]

I thought that \(\phi\) is the angle up and down, and \(\theta\) is the angle side to side. But, based on what you are saying it seems that I am wrong. I looked at the link you attached (thank you!) and I've been trying to figure it all out - but can you help me out?

I'm not suggesting you should redefine your angles, just asking you to tell me explicitly which they are as you are being taught.

I could guess easily that your [MATH]\phi[/MATH] is vertical and your [MATH]\theta[/MATH] is in the xy plane; what is not quite certain is where your [MATH]\phi[/MATH] starts from. My guess, based on your limits, is that it is a "latitude", measured from the "equator" (xy plane). If so, then think about what range it normally takes (in your class).

And regardless, do the visualization I suggested, in order to see what region you are integrating, and whether it should be corrected.

 

[burt]

I'm not suggesting you should redefine your angles, just asking you to tell me explicitly which they are as you are being taught.

I could guess easily that your [MATH]\phi[/MATH] is vertical and your [MATH]\theta[/MATH] is in the xy plane; what is not quite certain is where your [MATH]\phi[/MATH] starts from. My guess, based on your limits, is that it is a "latitude", measured from the "equator" (xy plane). If so, then think about what range it normally takes (in your class).

And regardless, do the visualization I suggested, in order to see what region you are integrating, and whether it should be corrected.

I started my \(\phi\) from the origin - just as I did with \(\theta\). When I do the visualization, it still seems correct to me. The shape is a bottom half of a circle - which seems to go from \(-\pi\) to \(0\).

 

[HallsofIvy]

Unfortunately, the use of \(\displaystyle \theta\) and \(\displaystyle \phi\) in polar coordinates in physics is the reverse of the use in mathematics.

 

[burt]

Unfortunately, the use of \(\displaystyle \theta\) and \(\displaystyle \phi\) in polar coordinates in physics is the reverse of the use in mathematics.

I don't understand.

 

[burt]

@Dr.Peterson
I see - I looked in this article and it says that \(\phi\) is the angle between the z axis and \(r\). Based on that, does it make sense to say that \(\frac{-\pi}{2}\leq\phi\leq 0\)?

 

[Dr.Peterson]

@Dr.Peterson
I see - I looked in this article and it says that \(\phi\) is the angle between the z axis and \(r\). Based on that, does it make sense to say that \(\frac{-\pi}{2}\leq\phi\leq 0\)?

That's what the limits would be if your definition was the latitude measured up and down from the xy plane, which is what I guessed you are using, based on your limits. In that case, your error was that you covered the entire semicircle at the bottom, which on rotating with [MATH]\theta[/MATH] would cover the hemisphere twice. When the equator is used, [MATH]\phi[/MATH] is generally taken to vary only between [MATH]-\frac{\pi}{2}\leq\phi\leq \frac{\pi}{2}[/MATH] so that it doesn't go past the z axis.

But in making that assumption, I was forgetting to look at your integrand. The fact that you used [MATH]\sin(\phi)[/MATH] implies that you are not using that definition!

The definition used in your integrand is what you said here, "the angle between the [positive] z axis and r"! It's also what's used in the page I referred you to before, except that they use r rather than [MATH]\rho[/MATH].) Then 0 means the "north pole", the equator is [MATH]\frac{\pi}{2}[/MATH], and the "south pole" is [MATH]\pi[/MATH]. Your limits then would be [MATH]\frac{\pi}{2}\leq\phi\leq \pi[/MATH]. Do you see the difference?

 

[burt]

That's what the limits would be if your definition was the latitude measured up and down from the xy plane, which is what I guessed you are using, based on your limits. In that case, your error was that you covered the entire semicircle at the bottom, which on rotating with [MATH]\theta[/MATH] would cover the hemisphere twice. When the equator is used, [MATH]\phi[/MATH] is generally taken to vary only between [MATH]-\frac{\pi}{2}\leq\phi\leq \frac{\pi}{2}[/MATH] so that it doesn't go past the z axis.

But in making that assumption, I was forgetting to look at your integrand. The fact that you used [MATH]\sin(\phi)[/MATH] implies that you are not using that definition!

The definition used in your integrand is what you said here, "the angle between the [positive] z axis and r"! It's also what's used in the page I referred you to before, except that they use r rather than [MATH]\rho[/MATH].) Then 0 means the "north pole", the equator is [MATH]\frac{\pi}{2}[/MATH], and the "south pole" is [MATH]\pi[/MATH]. Your limits then would be [MATH]\frac{\pi}{2}\leq\phi\leq \pi[/MATH]. Do you see the difference?

Thank you - I see - I was thinking about it backwards (or sideways) Your explanations helped a lot!
The other thing that helped was this video by Trefor Bazett. Thanks to you and him this has really been cleared up for me!

 

[burt]

When the equator is used, ϕϕ\displaystyle \phi is generally taken to vary only between −π2≤ϕ≤π2−π2≤ϕ≤π2\displaystyle -\frac{\pi}{2}\leq\phi\leq \frac{\pi}{2} so that it doesn't go past the z axis.

When the equator is not used, \(\phi\) only goes form \(0\) to \(\pi\), right?

 

[Dr.Peterson]

When the equator is not used, \(\phi\) only goes from \(0\) to \(\pi\), right?

Right.

As MathWorld said,

Define

to be the azimuthal angle in the

-plane from the x-axis with

(denoted

when referred to as the longitude),

to be the polar angle (also known as the zenith angle and colatitude, with

where

is the latitude) from the positive z-axis with

, and

to be distance (radius) from a point to the origin. This is the convention commonly used in mathematics.​