Using radians versus degrees when working with limits

C

CoachJones

New member
Joined
Apr 22, 2009
Messages
2
The lim {x->0} (sin3x)/x = 3. I know this is true because of L'Hoptial's rule. However, if I didn't know L'Hopital's, then I could put the limit into my graphing calculator, access the Table feature, and count by very, very small units -- watching what the table does as the function approaches 0. If I put my calculator in radians mode, I get 3 (that's great!). If I put my TI-84 in degree mode, I get 0.05235988. Why the discrepancy? Why would the limit as it approaches 0 be different in radians versus degrees since zero degrees is the same as zero radians? I know that all functions have domain in terms of real numbers and radians are real-valued angle representations. But don't degrees hold the same properties?
 
CoachJones said:
But don't degrees hold the same properties?
Click to expand...
Absolutely not. Radians are numbers.
‘Degrees’ are artifacts of a history.
They are products of poorly understood systems of measures.
The sine function maps real numbers to [-1,1].
Therefore, in the sin(x), x must be a real number.

In my former life I was obliged to attend many in-service mathematics education meetings. I always enjoyed creating a huge argument by expressing my firmly held view that ‘degrees’ should be banished from mathematics education.
 
I take it you feel the same about gradians, pka? :mrgreen:
 


There are two interpretations for the trigonometric functions; each lends itself to different applications.

When the ancient Greeks developed trigonometry (I think this word literally means something like "measurements of triangles"), it was for measuring static situations, like surveying, where angles do not change.

Somebody took one full rotation, and divided it up into 360 equal steps. Each step is 1 degree.

After the development of the calculus (in the 17th century), it was realized that trigonometry could be used in dynamic situations, like periodic motion, where angles undergo change (smoothly and continuously).

This is when the inputs had to change from degrees to radians because it's easy to use the Real number line to model these changing angles over a continuous spectrum (domain). I'm thinking that it would be a nightmare to achieve the same continuity with degrees.

(What values are between 1 degree and 2 degree? 60 minutes. What values are between two adjacent minutes? 60 seconds. What about between two adjacent seconds? Yikes!)

 
Correct me if I am wrong. But it seems to me that the system of degrees (360 degrees in a full circle) comes from the Babylonian number system.
They used a base 60 number system instead of base 10.

As someone who surveyed for years, I used degrees of course. Surveyors also use a measuring system which is measured in 1/100th of a foot instead of
fractions of an inch. i.e. 8 hundredths is about 1 inch, .67 is about 8 inches, and so forth.

Surveyors used to say inches are for carpenters and whores :D .

If you were to tell some of the old surveyors about radians, they would look at you like you were crazy. Though, I could have just as easily used them as degrees.

Same with the metric system. Very tabu to a lot of these old timers who are set in their ways. West Virginia began using the metric system in their highway blueprints a while back. I think they may have resorted back because of all the fuss raised about it.

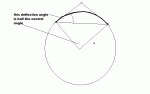
When I began surveying years ago, the friend that I helped who and had been doing it for years, used this formula to find angle of deflection in minutes per foot.

\(\displaystyle \frac{1718.875}{R}\). R is the radius of the curve. None of these guys ever bothered to ask or wonder where this came from, so I did.

It is, of course, derived from \(\displaystyle s=r{\theta}\) and converted to degrees. Here they were using radians all along and didn't know or even care.

All they knew is that it worked. Note, that if we divide 1718.875 by 60, we get something close to \(\displaystyle \frac{90}{\pi}\). It is one half because a deflection angle is one half the central angle of the circle the curve is an arc of.

\(\displaystyle \frac{\theta}{2}=\frac{90}{{\pi}r}\cdot s\)

That's all it was converted to degrees. No one ever thought to wonder where it came from. It was just magic.

Here is a diagram of what I am talking about. Sorry for being long winded. Just thought you may find it interesting.

Today's modern transits can be set to radians or even gradients if one wants. Remember the gradients?. During WWII, the contention was that American GI's

were to stupid to understand 360 degrees in a circle, so a system came out that used 400 degrees in a circle instead of 360. It is still on a lot of calculators.

So, you see, we can break a circle up into whatever pieces we like, but a radian is absolute no matter what 'degrees' are used.

I like pka's comments on degrees. That was put well. Let me try and explain to some of the surveying old-timers, though. They would shake their heads in disapproval and/or confusion.
 

Attachments

  • survey.gif
    survey.gif
    4.6 KB · Views: 378
AS Galactus pointed out the ancient Babylonians (Land of Sumer) use base 60 instead of base 10. They divided a circle into 360 degrees, the same time they estimated that the Earth rotated around the Sun. Of course they thought the rotation was a perfect circle instead of an ellipse (Kepler anyone) so they were off 5 days (1 year = 365 days and small change). The important thing here is that the Sumerians already knew that our solar system was heliocentric (everything revolved around the Sun) instead or the Catholic view that the solar system was geocentric (everything revolved around the Earth). Galieo put them straight (the Papists) and then was forced to recant to avoid being roasted. Fortunately he had friends in high places and spent the rest of his life as a recluse in house arrest. The ancient Chinese took it one step further, instead of advocating that the Earth was the center of the universe, they said that China was the center of the Universe and anything outside it was 2nd rate. The hubris of man.
 
Note to Daon

"gradians" is not the correct term.
It is "gradients", abbreviated as grad.
 
OK, so I was right in the beginning. I thought perhaps I misspelled it.
 


I'm thinking that the people of Babylon (as well as the entire extended region in what we now call the middle east) were Greeks in ancient times, but, then again, one of the three Ds that I received in high school was in History. :oops:

Looking at a map in a bible, it seems that Babylon was near the Euphrates River, south of Baghdad, Iraq. "Babylon" is Greek for "Babel" (a Hebrew name), as in "Tower of Babel".

Thanks for posting the extra information, everybody. It is interesting, and I enjoyed the humor, as well. (After learning of the Chinese proclamation, I wonder if the Vatican tried the same stunt, heh, heh. And, concerning the GIs, I've always cursed under my breath when trying to count individual degrees on a protractor. I hope those GIs had better eyesight than me.)

 
In reply to Galactus's lampoon on the G.I.'s of WW II. The Army had a system where 100 grads (what ever a grad was) equaled 90 degrees, thereby a complete circle equaled 400 grads. I was in the Army years ago and I soon learn that there were three ways to do anything, the right way, the wrong way, and the Army way. If you wanted to avoid going to Ft. Leavenworth for twenty years breaking big rocks into small rocks, you did everything the Army way, including trig.
 
The Babylonians were not the Greeks. Babylon was probably the first great empire. It fell to the Persians, which in turn fell to the Greeks, which in turn fell to the Romans, which in turn fell to the Barbarians.
 
Ok, I understand the difference between degrees and radians, BUT I still am confused about some stuff. (Maybe I worded the original question awkwardly).

Imagine the sin(0). You get 0. Are we talking about 0 degrees or 0 radians? It doesn't matter, you still get 0 when you find the sin of 0, no matter how 0 is measured.

Now Imagine lim {x-> 0} (sin x). For the sake of this argument, graph sin x on a graphing calculator and watch what happens as x approaches 0. It doesn't matter if you are in degrees or radians, because you get 0. Now imagine lim {x-> 0} (sin 3x). Same thing happens.

Now, however, now picture lim {x-> 0} (sin (3x))/x. Use your graphing calculator to see what happening when the limit is approaching 0. This time, it makes a difference if you are in degrees or radians.

If it didn't make a difference all of the other times, and if 0 degrees is the same things as 0 radians, why does dividing by x make a difference this time?
 
You must log in or register to reply here.
Top