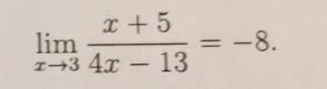Use the limit epsilon delta definition

[Fiestar]

so basically the exercise is to prove this.

Using the following definitions. For my exercise I have to use definition nr1. however I hit a road block where I get (33*|x-3|/|4x-13|) > epsilon. I have no idea how to get ride of |4x-13|

 

[tkhunny]

maximum(4x-13) on (2,4)?

 

[Fiestar]

I don't quite understand what u mean by your statement, could you elaborate?
and for those who wanted to see how far I got

 

[tkhunny]

$\displaystyle \iff |x-3| < \epsilon\cdot\dfrac{|4x-13|}{33}$

How big can |4x-13| be? It is unlimited. However, if we agree to ignore things too far away, we can limit the response.

Let's decide that we really don't care about large $\displaystyle \delta$. Maybe, $\displaystyle \delta = 1$ is as far as we care to consider. This gives us only $\displaystyle x\in(2,4)$. Thus, what is max(|4x-1|) on (2,4)?



Edit: Second thought, maybe 1 is too big. Let's keep it to 0.2 and avoid the singularity at 3.25.

 

[Fiestar]

okay so I should put a value from (2,4) into |4x-13|, but how do I choose which one to put? Is there a difference?

 

[Ishuda]

I don't quite understand what u mean by your statement, could you elaborate?
and for those who wanted to see how far I got

A little more detail than tkhunny initially gave: First we don't have to show for all delta, just that there exists one. So, if we can show that if x is between 2.9 and 3.1 exclusive [EDIT: I didn't catch it at first either, just assumed an interval (2,4) was ok. So reading tkhunny's next post, I changed the interval.] If we knew the minimum, call it A, of |x-13| in that interval we could say
$\displaystyle |\,{\frac{x-3}{x-13}}\,\,\, |\lt\, 33\, \frac{|x-3|}{A}$
thus
$\displaystyle {|x-3|}\, \lt\,\, \dfrac{A}{33}\,\, \epsilon$

That is not quite sufficient. Consider what delta you would choose if epsilon were very large, i.e. if epsilon were 3*10⁶, the above would give a delta of approximately 10⁶. If all we are going to do is restrict |x-3| to be less than 10⁶ [or even 20], our function would become unbounded on that interval.