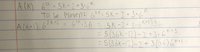Use of the inductive hypothesis and question of the correctness of a proof

[KrabLord]

Is this a true proof? I am curious about where I’ve placed the 36 in the last line; I am unsure if that proves the statement.

 

[HallsofIvy]

It appears that you want to prove, by induction, that \(\displaystyle 6^{2n}= 5n- 2+ 3\cdot 6^n\), for n any non-negative integer. Your basic problem is that what you are trying to prove simply is NOT true!
When n= 1, that says that \(\displaystyle 6^2= 5(1)- 2+ 3\cdot 6^1\). But the left side is 36 while the right side is 5- 2+ 18= 21.

 

[KrabLord]

It appears that you want to prove, by induction, that \(\displaystyle 6^{2n}= 5n- 2+ 3\cdot 6^n\), for n any non-negative integer. Your basic problem is that what you are trying to prove simply is NOT true!
When n= 1, that says that \(\displaystyle 6^2= 5(1)- 2+ 3\cdot 6^1\). But the left side is 36 while the right side is 5- 2+ 18= 21.

Sorry, I should have been more clear. I am not trying to prove \(\displaystyle 6^{2n}= 5n- 2+ 3\cdot 6^n\), but rather I am trying to prove\(\displaystyle 6^{2n}= 5k- 2+ 3\cdot 6^n\) for any natural number k and any natural number n

 

[HallsofIvy]

I thought the "5k" there was a typo. But "\(\displaystyle 6^{2n}= 5k- 2+ 3\cdot 6^n\)" for any natural number k and any natural number n" is, if anything, even more wrong! The left side of the equation depends on "n" only while the right side depends on both n and k. For any natural number, n, the left side is a fixed number while the right side varies depending on the value of k.

Are you trying, perhaps to prove that, for any natural number n, there exist a natural number k such that \(\displaystyle 6^{2n}= 5k- 2+ 3\cdot 6^n\). That would be the same as proving that \(\displaystyle 6^{2n}+ 2- 3\cdot 6^n\) is a multiple of 5.

 

[KrabLord]

I thought the "5k" there was a typo. But "\(\displaystyle 6^{2n}= 5k- 2+ 3\cdot 6^n\)" for any natural number k and any natural number n" is, if anything, even more wrong! The left side of the equation depends on "n" only while the right side depends on both n and k. For any natural number, n, the left side is a fixed number while the right side varies depending on the value of k.

Are you trying, perhaps to prove that, for any natural number n, there exist a natural number k such that \(\displaystyle 6^{2n}= 5k- 2+ 3\cdot 6^n\). That would be the same as proving that \(\displaystyle 6^{2n}+ 2- 3\cdot 6^n\) is a multiple of 5.

Yes, that’s the goal. I want to know if my (36) is acceptable, though.

 

[Dr.Peterson]

I think you need to start over, stating exactly what it is that you are trying to prove. The work you showed is inconsistent with what you are saying now, as you appear to be doing induction on k, not n.

 

[JeffM]

I am still not sure that we understand what is to be proved because the proof given has nothing to do with what has been discussed in the preceding posts. We ask that you quote exactly and completely the statement of the problem in your first post for good reason. The proof given is facially incorrect because it does not even prove the base case.

I am going to assume that a complete statement would be something like:

[MATH]\text {PROVE: } n \in \mathbb Z^+ \implies \exists \ k_n \in \mathbb Z^+ \text { such that } 6^{2n} = 5k_n - 2 + 3 * 6^n.[/MATH]
Before trying to prove something by induction, it is often helpful to explore the first few cases numerically. First, it will certainly prove or disprove the base case. Second, it will frequently provide clues about how to do a proof by induction.

[MATH]6^{(2*1)} - 3 * 6^1 + 2 = 36 - 18 + 2 = 18 + 2 = 20 = 5 * 4.[/MATH]
[MATH]6^{(2*2)} - 3 * 6^2 + 2= 1296 - 108 - 2 = 1188 + 2 = 1190 = 5 * 238.[/MATH]
[MATH]6^{(2*3)} - 3 * 6^3 + 2 = 46656 - 648 + 2 = 46008 + 2 = 46010 = 5 * 9202.[/MATH]
So it seems to be true, we have the base case, and, after staring at it a while, I see a pattern worth exploring.

Can you see a pattern? Do you need a hint?

 

[KrabLord]

I am still not sure that we understand what is to be proved because the proof given has nothing to do with what has been discussed in the preceding posts. We ask that you quote exactly and completely the statement of the problem in your first post for good reason. The proof given is facially incorrect because it does not even prove the base case.

I am going to assume that a complete statement would be something like:

[MATH]\text {PROVE: } n \in \mathbb Z^+ \implies \exists \ k_n \in \mathbb Z^+ \text { such that } 6^{2n} = 5k_n - 2 + 3 * 6^n.[/MATH]
Before trying to prove something by induction, it is often helpful to explore the first few cases numerically. First, it will certainly prove or disprove the base case. Second, it will frequently provide clues about to do a proof.

[MATH]6^{(2*1)} - 3 * 6^1 + 2 = 36 - 18 + 2 = 18 + 2 = 20 = 5 * 4.[/MATH]
[MATH]6^{(2*2)} - 3 * 6^2 + 2= 1296 - 108 - 2 = 1188 + 2 = 1190 = 5 * 238.[/MATH]
[MATH]6^{(2*3)} - 3 * 6^3 + 2 = 46656 - 648 + 2 = 46008 + 2 = 46010 = 5 * 9202.[/MATH]
So it seems to be true, we have the base case, and, after staring at it a while, I see a pattern worth exploring.

Can you see a pattern? Do you need a hint?

I see the pattern. I meant for the entire post to be about asking if it is acceptable to put the 36 where I did, ie, if that proves the statement. My feeling is that it does not.

here is the problem from the book, but I am still mainly interested in the 36.

 

[lev888]

I see the pattern. I meant for the entire post to be about asking if it is acceptable to put the 36 where I did, ie, if that proves the statement. My feeling is that it does not.

here is the problem from the book, but I am still mainly interested in the 36.

Now that we have the problem statement please show the solution of that problem. Your question regarding 36 is not clear.

 

[KrabLord]

Now that we have the problem statement please show the solution of that problem. Your question regarding 36 is not clear.

Is this a true proof? I am curious about where I’ve placed the 36—the very last 36—in the last line; I am unsure if that proves the statement.

 

[KrabLord]

I do not care about the problem. I only care about the 36.

 

[KrabLord]

I do not care about the problem. I only care about the 36.

The k is just “there exists natural number k such that” the statement is true

 

[lev888]

I do not care about the problem. I only care about the 36.

Are you asking whether this is a correct equality: 6^k+3 = 36*6^k+1?
The answer is yes.
Are you asking whether 36 "proves the statement"? The answer is no idea, since I don't understand the question.

 

[Dr.Peterson]

We can't tell you whether the 36 does what you need it to do, when it is in the midst of a proof that is so invalid (specifically, because you are using k to mean two different things) that we can't be sure what you are trying to accomplish.

Certainly it is true that [MATH]6^{2k+2} = 6^{2k}\cdot 36[/MATH], and that [MATH]6^{k+3} = 6^{k+1}\cdot 36[/MATH], if that is all you are asking. But it can't prove anything in an invalid context.

 

[JeffM]

Because the OP has marked the question solved, we can go ahead and sketch A proof by induction.

The following lemma is easily proved by induction.

[MATH]\text {LEMMA I: } n \in \mathbb Z^+ \implies \exists \ p_n \in \mathbb Z_{\ge 0} \text { such that } 6^n = 5p_n + 6.[/MATH]
Obviously p_1 = 0. So there is a non-empty set S such that, for arbitrary element a,

[MATH]a \in \mathbb S \implies a \in \mathbb Z^+ \text { and } \exists \ p_m \in \mathbb Z_{\ge 0} \text { such that } 6^m = 5p_m + 6.[/MATH]
[MATH]a + 1 \in \mathbb Z^+ \ \because \text { the non-negative integers are closed under addition.}[/MATH]
[MATH]6^{(a + 1)} = 6 * 6^a = 6 * (5p_a + 6) = 30p_a + 30 + 6 = 5(6p_a + 6) + 6.[/MATH]
[MATH]\therefore p_{a+1} = 6p_a + 6 \in \mathbb Z_{\ge 0} \text { Q.E.D.}[/MATH]
From there it is easy to prove these two lemmas without induction.

[MATH]\text {LEMMA II: } n \in \mathbb Z^+ \implies \exists \ q_n \in \mathbb Z \text { such that } 3 * 6^n = 5q_n + 8.[/MATH]
[MATH]\text {LEMMA III: } n \in \mathbb Z^+ \implies \exists \ r_n \in \mathbb Z \text { such that } 6^{(2n)} = 5r_n + 6.[/MATH]
From there the proof of the theorem is a cinch.

[MATH]6^{(2n)} + 2 - 3 * 6^n = 5r_n + 6 + 2 - (5q_n + 8) = 5(r_n - q_n).[/MATH]
[MATH]\text {Let } k_n = (r_n - q_n).[/MATH]
[MATH]\therefore k_ n \in \mathbb Z \text { and }[/MATH]
[MATH]6^{(2n)} = 5k_n - 2 + 3 * 6^n.[/MATH]
We only need induction for Lemma I.