Jakotheshadows
New member
- Joined
- Jun 29, 2008
- Messages
- 47
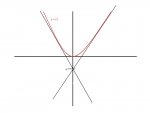
"Draw a diagram to show that there are two tangent lines to the parabola y = x^2 that pass through the point (0, -4). Find the coordinates of the points where these tangent lines intersect the parabola."
I know that y'= 2x by the power rule, but I'm not sure how to find the points where these specific undetermined tangents intersect the parabola. There's something I'm just not seeing, and I really need to know how to start working on this. Is there some way to determine what these tangents are with the knowledge that they both pass through (0, -4) and that they are tangent to y=x^2 at some unknown point? (mspaint ftw )
)
I know that y'= 2x by the power rule, but I'm not sure how to find the points where these specific undetermined tangents intersect the parabola. There's something I'm just not seeing, and I really need to know how to start working on this. Is there some way to determine what these tangents are with the knowledge that they both pass through (0, -4) and that they are tangent to y=x^2 at some unknown point? (mspaint ftw