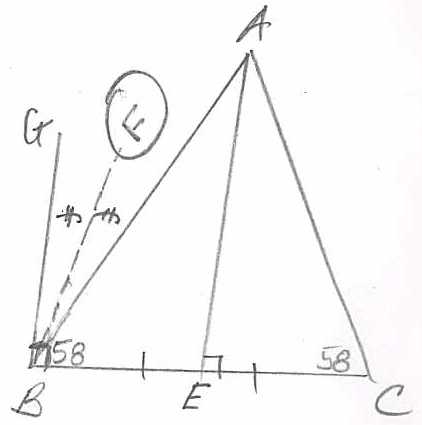
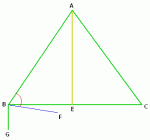
In the figure below, we are given the following statements:
(a) m angle ACE = 58 degrees.
(b) AE is the perpendicular bisector of BC.
(c) BF is the bisector of ABG.
(d) GB is perpendicular to BE.
(The picture is that of a triangle with bisector down middle and also on the end is the angle GB with bisector BF)
Prove that m angle FBG = 74 degrees. (State all the statements that are necessary in your proof along with their reasons in a two-column table.)
(a) m angle ACE = 58 degrees.
(b) AE is the perpendicular bisector of BC.
(c) BF is the bisector of ABG.
(d) GB is perpendicular to BE.
(The picture is that of a triangle with bisector down middle and also on the end is the angle GB with bisector BF)
Prove that m angle FBG = 74 degrees. (State all the statements that are necessary in your proof along with their reasons in a two-column table.)