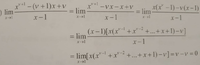Trying to solve a really strange limit

[HazyMan]

The exercise simply says: "Find the limits" and it shows 3 questions. My point of interest is just one of the three questions which is a lot different. The question is:
lim as x->1 of [x^v+1-(v+1)x+v]/x-1.

What confuses me is the whole v+1 concept. I tried looking through a solution book that was designed for these questions and i still can't exactly understand this. How can the limit be found? I'm aware that Polynomial related skills must be familiarized, but i really can't grasp this. Thanks for reading!

 

[Steven G]

Can you please write the problem showing what you are dividing by? What you wrote is [x^v+1-(v+1)x+v]/ x and then subtract 1.

The problem is hinting that for any v, this limit will be the same OR maybe the limit will depend on v.

I suspect that you plugged in 1 for x in [x^v+1-(v+1)x+v]/(x-1) and got 0/0.
If you showed your work, which IS required to receive help or at least told us which course you are in we would know if you know/should know L'hopital's rule. I will assume you do.

Did the problem state anything about v, like v is a positive integer or anything?

 

[HazyMan]

Hello, I made a mistake. I am dividing by x-1 as a whole

 

[Steven G]

Hello, I made a mistake. I am dividing by x-1 as a whole

Yes, I know. I even wrote that when explaining how to attack this problem. Just use parenthesis when writing x-1, ie write (x-1).
The main problem here is that you still have not shown any work, did not say which calculus you are in and did not inform us if you know L'hopital rule. Is there is reason for this?

 

[JeffM]

When you don't know what to do, experiment.

[MATH]\text {ASSUME } x \ne 1 \text { but } x \approx 1.[/MATH]
[MATH]v = 0 \implies \dfrac{x^{(v+1)} - (v + 1)x + v}{x - 1} = \dfrac{x^{(0+1)} - (0 + 1)x + 0}{x - 1} = \dfrac{0}{x - 1} = 0.[/MATH]
[MATH]v = 1 \implies \dfrac{x^{(v+1)} - (v + 1)x + v}{x - 1} = \dfrac{x^2 - 2x + 1}{x - 1} = \dfrac{(x - 1)^2}{x - 1} = x - 1 \approx 0.[/MATH]
[MATH]v = 2 \implies \dfrac{x^{(v+1)} - (v + 1)x + v}{x - 1} = \dfrac{x^3 - 3x + 2}{x - 1} =[/MATH]
[MATH]\dfrac{(x - 1)(x^2 + x - 2)}{x - 1} = x^2 + x - 2 \approx 0.[/MATH]
Now I do not know whether this is a clue to the correct answer because we are here to help, not do the work. But it does suggest something to try. Actually using math often involves experimenting until you find a good path.

 

[HazyMan]

Yes, I know. I even wrote that when explaining how to attack this problem. Just use parenthesis when writing x-1, ie write (x-1).
The main problem here is that you still have not shown any work, did not say which calculus you are in and did not inform us if you know L'hopital rule. Is there is reason for this?

Alright, i do not know L'hopital's rule, i don't like in the US so i don't understand what you mean when you say "Which Calculus", but long story short i'm just exercising limit exercises.

Anyway here's the work that i have done and let me show you how the solution book worked on the problem:

 

[HazyMan]

When you don't know what to do, experiment.

[MATH]\text {ASSUME } x \ne 1 \text { but } x \approx 1.[/MATH]
[MATH]v = 0 \implies \dfrac{x^{(v+1)} - (v + 1)x + v}{x - 1} = \dfrac{x^{(0+1)} - (0 + 1)x + 0}{x - 1} = \dfrac{0}{x - 1} = 0.[/MATH]
[MATH]v = 1 \implies \dfrac{x^{(v+1)} - (v + 1)x + v}{x - 1} = \dfrac{x^2 - 2x + 1}{x - 1} = \dfrac{(x - 1)^2}{x - 1} = x - 1 \approx 0.[/MATH]
[MATH]v = 2 \implies \dfrac{x^{(v+1)} - (v + 1)x + v}{x - 1} = \dfrac{x^3 - 3x + 2}{x - 1} =[/MATH]
[MATH]\dfrac{(x - 1)(x^2 + x - 2)}{x - 1} = x^2 + x - 2 \approx 0.[/MATH]
Now I do not know whether this is a clue to the correct answer because we are here to help, not do the work. But it does suggest something to try. Actually using math often involves experimenting until you find a good path.

setting v as an actual number was exactly what i thought of, but since the solution book uses a very strange and different solution (ive posted an image) i thought that maybe setting v as an interger wouldn't be "accepted", supposing the question was included on an exam.

 

[Steven G]

Alright, i do not know L'hopital's rule, i don't like in the US so i don't understand what you mean when you say "Which Calculus", but long story short i'm just exercising limit exercises.

Anyway here's the work that i have done and let me show you how the solution book worked on the problem:

In the US we have Calculus 1, Calculus 2 and Calculus 3. In Calculus 2 you learn about L'hopital's rule and this procedure make this limit easy to solve.
So the solution does show that doing the division works. What part of the solution are you not understanding?

 

[HazyMan]

It's the last 2 parts of the solution that I do not understand at all.

 

[Dr.Peterson]

Are you aware of factoring a difference of squares or a difference of cubes?

[MATH]a^2 - b^2 = (a - b)(a + b)[/MATH]​

[MATH]a^3 - b^3 = (a - b)(a^2 + ab + b^2)[/MATH]​

They are using the generalization of that fact:

[MATH]a^n - b^n = (a - b)(a^{n-1} + a^{n-2}b + ... + ab^{n-2} + b^{n-1})[/MATH]​

 

[HazyMan]

Are you aware of factoring a difference of squares or a difference of cubes?

[MATH]a^2 - b^2 = (a - b)(a + b)[/MATH]​

[MATH]a^3 - b^3 = (a - b)(a^2 + ab + b^2)[/MATH]​

They are using the generalization of that fact:

[MATH]a^n - b^n = (a - b)(a^{n-1} + a^{n-2}b + ... + ab^{n-2} + b^{n-1})[/MATH]​

I am aware but i hate having to memorize a^3−b^3. Even if i took that into full consideration i totally wouldn't be able to come up with that final formula.

 

[Dr.Peterson]

You can actually generate the formula by long division (at least enough to see the pattern, if not to conclusively prove it in general). That's especially true of the special case involved in your problem: [MATH]a^n - 1 = (a - 1)(a^{n-1} + a^{n-2} + ... + a + 1)[/MATH]. Just divide [MATH]a^n - 1[/MATH] by [MATH]a-1[/MATH].

Or, since it is a very clear pattern, you can just write it out and check it by multiplication, observing how everything but the first and last terms cancel.

 

[JeffM]

I am aware but i hate having to memorize a^3−b^3. Even if i took that into full consideration i totally wouldn't be able to come up with that final formula.

The point is not to memorize that one fact. It is to memorize an infinite set of patterns.

[MATH]n \in \mathbb N_0 \text { and } n \ge 1 \implies a^n - b^n = (a - b) * \sum_{k=0}^{n-1} a^{(n-1-k)}b^k.[/MATH]
And that implies another infinite pattern.

[MATH]n \in \mathbb N_0 \text { and } n \ge 1 \implies a^n - 1 = a^n - 1^n = (a - 1) * \sum_{k=0}^{n-1} a^{(n-1-k)}.[/MATH]