Nathanhale
New member
- Joined
- Dec 27, 2015
- Messages
- 2
Hi folks. I am new here and this is my first post. I am trying to understand calculus. Please look at the problem below.I got it from a calculus site. My question is very simple. Shouldn't the amount of water coming out of the faucet be 10 gallons even? I am plugging in "2" in the "t". Where am I thinking wrong?
Thank you for your time and help.
----------------------------
A faucet is turned on and water flows out at a rate of
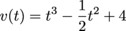
gallons per minute, where t is the number of minutes since the faucet was turned on. To the nearest gallon, how much water flows out of the faucet during the first two minutes the faucet is turned on?
Answer
We want to know the change in the amount of water that has come out of the faucet from time t = 0 minutes to time t = 2 minutes. This means we need to integrate v(t) from 0 to 2.
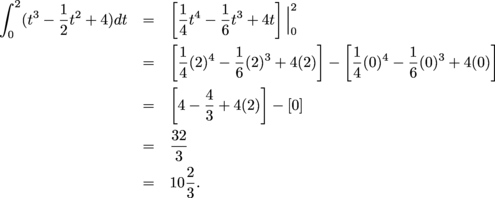
Rounding to the nearest gallon, 11 gallons come out of the faucet during the first 2 minutes it is turned on
Thank you for your time and help.
----------------------------
A faucet is turned on and water flows out at a rate of
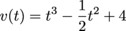
gallons per minute, where t is the number of minutes since the faucet was turned on. To the nearest gallon, how much water flows out of the faucet during the first two minutes the faucet is turned on?
Answer
We want to know the change in the amount of water that has come out of the faucet from time t = 0 minutes to time t = 2 minutes. This means we need to integrate v(t) from 0 to 2.
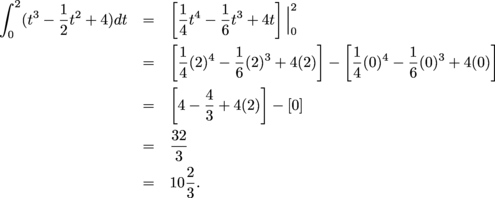
Rounding to the nearest gallon, 11 gallons come out of the faucet during the first 2 minutes it is turned on
