Trouble with Min, Max, and Inflection Points

[SeekerOfDragons]

I'm having some major issues trying to solve the following:

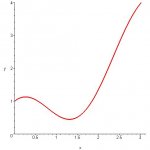
find all local extrema and inflection points of:

f(x) = x + cos(2x) 0<= X <= Pi

I got f'(x) = 1 - 2 sin(2x)

f"(x) = -4 cos(2x)

I can't figure out how to solve the above for 0. through plug and play I figured out one of the inflection points to be Pi/4. I can't figure out how to get the max/min points. can't figure out how to get sin(2x) = 1/2

any hints, tips, solutions would be much appreciated

 

[BigGlenntheHeavy]

\(\displaystyle f(x) \ = \ x+cos(2x), \ 0 \ \le \ x \ \le\pi\)

\(\displaystyle f \ ' \ (x) \ = \ 1-2sin(2x), \ 2x \ = \ arcsin(1/2), \ 2x \ = \ \frac{\pi}{6},\frac{5\pi}{6}, \ x \ = \ \frac{\pi}{12},\frac{5\pi}{12}.\)

\(\displaystyle f(0) \ = \ 1, \ endpoint\)

\(\displaystyle f(\pi/12) \ = \ \frac{\pi+6\sqrt3}{12}, \ Rel. \ Max.\)

\(\displaystyle f(5\pi/12) \ = \ \frac{5\pi-6\sqrt3}{12}, \ Absolute \ Min.\)

\(\displaystyle f(\pi) \ = \ \pi+1, \ Absolute \ Max\)

\(\displaystyle f \ " \ (x) \ = \ -4cos(2x), \ 2x \ = \ arccos(0), \ 2x \ = \ \frac{\pi}{2},\frac{3\pi}{2}, \ x \ = \ \frac{\pi}{4},\frac{3\pi}{4}\)

\(\displaystyle Points \ of \ inflection: \ (\frac{\pi}{4},\frac{\pi}{4}),(\frac{3\pi}{4},\frac{3\pi}{4})\)

See graph:

[attachment=0:1mxbci5z]zip.jpg[/attachment:1mxbci5z]