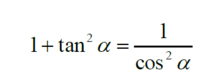Hello.
Trying to figure out how to calculate the following limit.
I got "0/0" kind of limit and we are not allowed to use l'hopital yet.
I thought the following trigonometric identity might help but I ended up with a wrong answer.
might help but I ended up with a wrong answer.
1st, I cant figure out where is my mistake (it is certainly there)
2nd, any suggestions for calculating this Limit ?

This is my best attempt (which is wrong)

Trying to figure out how to calculate the following limit.
I got "0/0" kind of limit and we are not allowed to use l'hopital yet.
I thought the following trigonometric identity
 might help but I ended up with a wrong answer.
might help but I ended up with a wrong answer.1st, I cant figure out where is my mistake (it is certainly there)
2nd, any suggestions for calculating this Limit ?

This is my best attempt (which is wrong)