Trigonometric functions in a quadrant using CAST RULE
- Thread starter Vikash
- Start date
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,975
Are you really saying that you are posting questions at this level and you don't know about odd & even functions?
Any function having the property that \(f(-x)=-f(x)\) for all \(x\) is an odd function; Any function having the property that \(g(-x)=g(x)\) for all \(x\) is an even function.
EXAMPLES: \(f(x)=x+6x^3\) is an odd function; \(g(x)=x^2+2\) is an even function; \(k(x)=1+x+x^2\) is neither ever nor odd.
The sine function is odd and cosine function is even.
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,605
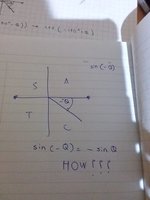
I dislike mnemonics like "CAST", but in those terms, you've drawn [MATH]-\theta[/MATH] in the fourth quadrant, which is labeled as C, which means that only the Cosine, of the three main functions, is positive. Therefore the sine is negative; and since both [MATH]\theta[/MATH] and [MATH]-\theta[/MATH] have the same reference angle, [MATH]\sin(-\theta) = -\sin(\theta)[/MATH].
(By the way, the proper spelling is "theta", not "thetha".)
The way I find it easiest to understand all this (answering your "why?" question in the bigger sense, not just "How would I decide this?"), the definition of the sine, for an angle whose terminal ray passes through a point [MATH](x, y)[/MATH], is [MATH]\sin(\theta) = \frac{y}{r}[/MATH], where [MATH]r[/MATH] is the distance to the point, [MATH]\sqrt{x^2 + y^2}[/MATH]. The negative angle is reflected over the x-axis, so [MATH]x[/MATH] stays the same, and [MATH]y[/MATH] changes to [MATH]-y[/MATH]. As a result, [MATH]r[/MATH] is also unchanged, and [MATH]\sin(-\theta) = \frac{-y}{r} = -\frac{y}{r} = -\sin(\theta)[/MATH].