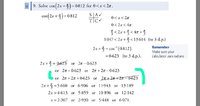
First of all the domain is NOT 2pi. 2pi is just one value and the entire domain is what x can be. x can be any value between 0 and 2pi.
For example, note that cos(2x+pi) = .5 has an infinite number of solutions. Please graph the cos(x) which goes from -infinity<x<infinity to verify that. That is the graph goes all the way to the left and all the way to the right of the origin AND IT REPEATS. So if there is one solution to cos(x) = .5 than there are an infinite number of solutions. Suppose r and s are two different solutions for x between 0 and 2pi. Then what are others. The cosine (and sine) function repeats every 2pi units. That is cos(r)= cos(r + 1*2pi) = cos (r+2*2pi) = cos (r +3*2pi) =....= cos(r - 1*2pi) = cos (r-2*2pi) = cos (r -3*2pi) =....=cos(s + 1*2pi) = cos (s+2*2pi) = cos (s +3*2pi) =....= cos(s - 1*2pi) = cos (s-2*2pi) = cos (s -3*2pi) =...=.5
For r we get r, r+2pi, r+4pi, r+6pi, ..., r-2pi. r-4pi, r-6pi, ... And for s we get s, s+2pi, s+4pi, s+6pi, ..., s-2pi. s-4pi, s-6pi,... as solutions to cos(2x+pi) = .5.
So we set 2x+pi = r, solve for x and if x is between 0 and 2pi we keep this solution ((r-pi)/2)
Then we set 2x+pi = r+2pi and solve for x. We keep this solution if x is between 0 and 2pi.
We continue until it becomes clear that no more of this type will work. The we try r-2pi, r-4pi, etc. Then do the same for s.