Trigonometric equations question

P

parakeet

New member
Joined
Jan 8, 2009
Messages
9
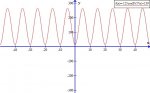
*I'm working with a ferris wheel
* Diameter is 250 ft
* Every ten minutes it makes a full rotation.

Now I figured out the amplitude was 250.

Then it asks me for the period of my curve. How do I find that? I was told you find it using this equation:

2PIE divided by period = b

I can't really use this if I don't know the period or know what b stands for.

Also, I'm supposed to write a cosine equation. I have a sin equation...how do I get my cosine equation? My sin equation is:
125sin(.01047197551196x-1.5707963267949) +125 = Y
Help would be greatly appreciated.


Notes:

I found 5 critical t values and I have my sin graph because of that.

I can't figure out if the amplitude is 125 or 250... What is it? I'm leaning for 250 since that's the peak of the ferris wheel.

How do I get the period? I THINK it's 250...although i'm not sure.

How do I get a cosine equation when I have the sin equation already?
 
Note that \(\displaystyle sin(Ax-\frac{\pi}{2}) = -cos(Ax)\)

And never spell \(\displaystyle {\pi}\) as 'PIE' again. Those that do get sent to a work camp. :wink:

The period is one complete revolution of the wheel. In this case, one rev. every 1/6 hours

You can use \(\displaystyle y=Acos(B(x-C))+D\)

A=amplitude or distance from centerline of graph to max or min. The distance between the max and min divided by 2. Which is 125, you are right.

\(\displaystyle B=\frac{2\pi}{\text{period}}\)

C=horizontal shift or time to reach first max point.

D=vertical shift or the distance the center of the wheel is from the ground.

\(\displaystyle \text{period}=\frac{2\pi}{B}\)

Since it has one rotation every 10 minutes, it rotates \(\displaystyle 12\pi\) radians per hour.
 
Sorry about that, I forgot it was PI.

Alright, so I was told that the wheel is 14 feet off the ground. So does that mean I need to add 125 and 14 making 139 ft to get the distance from the center of the ground?

Okay so we have:

Y= 125cos ...

Then B = 2PI over the period as you said so...

B = 360 degrees over 1/6 so that's 60.

Y = 125cos60

It reaches it's first max point at 5 minutes so that's

Y = 125cos60(x-5) + 139

Is this my equation or did I go wrong somewhere?

Thank you.
 
So my equation is right, right?

'D=the distance the center of the wheel is from the ground.'

The wheel is attached to some stick that is 14 ft off the ground. Then from there, you're at the bottom of the wheel. You need to travel to the radius which is 125ft after traveling the 14ft that the wheel is sitting on.

Y = 125cos60(x-5) + 139 ?


I think the 60 in there is wrong, isn't it? I mean...

12PI per hour means 2pi in ten minutes. My period is 2pi?
 
It makes one rev of 2Pi every 10 minutes. That is \(\displaystyle \frac{2\pi}{10}=\frac{\pi}{5}\) rad per minute.

I am sorry, I am stupid. You were right. It is 139 for D. 14+125=139.

So, we get \(\displaystyle y=-125cos(\frac{\pi}{5}t)+139\)
 
It's okay!

You're anything BUT stupid!

So my period is ten minutes?

So the equation I am looking for is...

Y = 125cos ( PI/5 ( x - 5 minutes ) ) + 139 ?
 
I edited my post:

\(\displaystyle y=-125cos(\frac{\pi}{5}t)+139\)

Check it against some times. At t=0, we get 14. That is when the wheel is at the bottom of its rotation.

Try 5 minutes. Then it should be at the top. Half way around. Plug in t=5 we get 264. Which is 250+14=264.

At 10 minutes it should be back around at the bottom. We get 14 at t=10.

How high is it at 1/4the the rotation or in 2.5 minutes?. 139. Which is 125+14 as it should be.

See now?.

For the sine version.

\(\displaystyle y=125sin(\frac{\pi}{5}t-\frac{\pi}{2})+139\)
 
Sorry, I'm a VERY slow learner.

\(\displaystyle y=-125cos(\frac{\pi}{5}t)+139\)

Where did your X go?
 
BTW, your set up is also OK. It is the same as mine.

\(\displaystyle -125cos(\frac{\pi}{5}t)+139=125cos(\frac{\pi}{5}(t-5))+139\)

That is OK. I just used t instead of x to represent time.
 
To post a picture or diagram use the Manage attachments option. The IMG tags are not necessary.

I am using LaTex to post in the nice math format. Click on 'quote' to see the code I typed to get it to display that way.
 
The thing is that I need to graph these equations. When I try graphing both mine and yours, neither seems to work.
 
Make sure your calculator is not in degrees and you're using radians or vice versa.

Here is the graph of the cosine.
 

Attachments

  • ferris.jpg
    ferris.jpg
    33.6 KB · Views: 303
Hey, how about doing a Google for it. I once found a nice applet for Ferris wheels. It is animated and drew the graphs when you plug in the data. If I remember correctly, it was pretty nice.
 
When doing that, what was your window range?


Also, I see this little thing between the 5 and X, what is that?

I'll look for that.
 
That's just multiplication. As in 5*5=25. Come on kid :roll: :wink: .

I used -50 to 50 for x. The y can be whatever fits. Try -300 to 300.

All set now?. You can use * for multiplication whenever need be. In this case, Pi/5 times t is Pi/5*t
 
Haha, sorry. I got that a couple of seconds after I finished typing that up. Forgot to edit.


Yeah, I found the appropiate window range.

Now say I'm asked at what time will the wheel reach the following height, then what steps do I follow?

I started doing trace with the calculator find out when it would reach 240 ft but then I found out that's not very realiable.

http://math.rice.edu/~pcmi/sphere/degrad.gif

I'm trying to use this thing but ehh... how do I figure it out?

I know circumference is 785.4 ft. so...

Wait, when it gets to 250 it's been 5 minutes.

At four minutes, it's been... 200 ft?

240 is 40 away from 200.

So it'll take 4 minutes and 4/5 minutes? So that's 4 minutes and 48 seconds? Is my logic alright ?

Damnit, I forgot about adding the 14. Well, is this method going to work?
-----------


I want 240 ft



264 ft = 5 min

52.8 ft. = 1 min

That means that 4 mins = 211.2

240 ft is 24 away from 5 mins so it’s

4 mins and 24/52.8 minutes that being


4 minutes and 27 seconds ?
 
Set your equation equal to 240 and solve for x (t, in my case).

\(\displaystyle 240=-125cos(\frac{\pi}{5}x)+139\)

\(\displaystyle \frac{-101}{125}=cos(\frac{\pi}{5}t)\)

\(\displaystyle cos^{-1}\left(\frac{-101}{125})=\frac{\pi}{5}x\)

\(\displaystyle x=\frac{5cos(\frac{-101}{125})}{\pi}\approx 3.997 \;\ minutes\)

This will give the number of minutes until it reaches 240 feet. Now, remember, at 5 minutes it is at 264 feet.

Also, we need the time on the other side of the wheel when it is heading back down. Then, it will be a little more than 5 minutes.

Subtract the last value from 10 minutes.

\(\displaystyle 10-3.997=6.003 \;\ minutes.\)

We could find a general formula, but it is rather unnecessary since it repeats every 10 minutes.
 
You must log in or register to reply here.
Top