amathproblemthatneedsolve
Junior Member
- Joined
- May 12, 2019
- Messages
- 189
Tom wants to sell some land, ( the diagram below) Before he can sell the land, he needs to install a pipe which costs $50 per meter. A property developer is only interested if the block of land can be subdivided into four sections of at least 700 square meters (700 m^2 ) each. The straight pipe goes from point A to C (shown as - - - - - on the diagram). This pipe must be one of the boundaries for all four sections so that each section can have easy access to this pipe. activity requires you to provide necessary calculations and write a report to determine if the subdivision meets the property developer’s requirements.
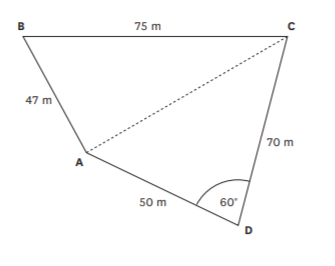 The land for sale is bounded by ABCD and needs to be split into four sections. The pipe running through the land is between points A and C (shown as - - - - - ) and each of the four sections must-have part of AC as one of its boundaries.
The land for sale is bounded by ABCD and needs to be split into four sections. The pipe running through the land is between points A and C (shown as - - - - - ) and each of the four sections must-have part of AC as one of its boundaries.
1. Calculate the length and cost of the pipe going through the land from point A to point C. Would this be the length?
If I solved that correctly how do I start on part 2 and 3?
2. Demonstrate that the land can be divided into four sections each of more than 700 m2 in order to meet the buyer’s requirements for the sale to proceed.
3. The buyer has also decided that he will not purchase the land if all of the sections are triangular. Produce a report justifying the sale of the land showing one possible way of dividing the land into four sections each of more than 700 m^2 . show the dimensions of each of the sections.

1. Calculate the length and cost of the pipe going through the land from point A to point C. Would this be the length?
If I solved that correctly how do I start on part 2 and 3?
2. Demonstrate that the land can be divided into four sections each of more than 700 m2 in order to meet the buyer’s requirements for the sale to proceed.
3. The buyer has also decided that he will not purchase the land if all of the sections are triangular. Produce a report justifying the sale of the land showing one possible way of dividing the land into four sections each of more than 700 m^2 . show the dimensions of each of the sections.


