alohadressage
New member
- Joined
- Jun 13, 2008
- Messages
- 2
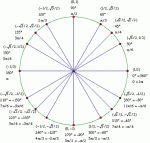
i cant remember what these are called, but you know that formula where like, if (x^2+y^2)^1/2=r^2, then sin=x/r, cos=y/r, or something like that? well, i cant remember what sin, cos, tan, cosec, sec, and cot equal...can anyone please tell me?
: ] thanks...
: ] thanks...